标签:
最短路
最短路有多种算法,常见的有一下几种:Dijstra、Floyd、Bellman-Ford,其中Dijstra和Bellman-Ford还有优化;Dijstra可以用优先队列(或者堆)优化,Bellman-Ford也可以用队列优化,通常称为spfa。下面分别对这几种算法进行说明。
Dijstra适用于没有负权边的图,Bellman-Ford适用于有负权边的图,但是不能得到有负环的图的最短距离,只能判断有没有负环。Dijstra和Bellman-Ford都是单源最短路,Floyd算法是多源最短路。
一、Dijstra算法
Dijstra算法是不断将新的距离原点最短的点加入已经得到最短距离的集合,然后每加入一个点都更新各个点到源点的距离。这里有一个问题,设已经的到最短距离的点的集合为V,如何保证已经加入V的点已经得到了最短距离而之后源点到V中的点的最短距离不会改变了呢?假设i点已经加入V,而j点后来加入V,因为所有的边权值都是正的,如果存在dis[j]+cost[j][i]<dis[i](dis[i]表示i点到源点的距离,cost[i][j]表示i点到j点的边的权值),那么dis[j]<dis[i],如果dis[j]<dis[i],j点就应该先于i点加入V,与已知条件不符。所以在i点加入V之后,不会存在一个点作为中间点使得源点到i点的距离最小。
Dijstra算法的过程如下:
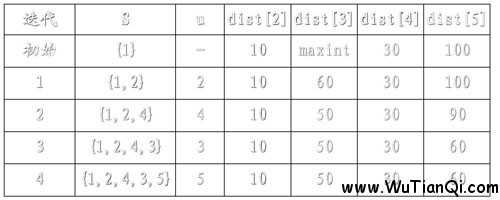
代码:

/* * 单源最短路径,Dijkstra算法,邻接矩阵形式,复杂度为O(n^2) * 求出源beg到所有点的最短路径,传入图的顶点数,和邻接矩阵cost[][] * 返回各点的最短路径lowcost[], 路径pre[].pre[i]记录beg到i路径上的父结点, pre[beg]=-1 * 可更改路径权类型,但是权值必须为非负 * */ const int MAXN=1010; #define typec int const typec INF=0x3f3f3f3f;//防止后面溢出,这个不能太大 bool vis[MAXN]; int pre[MAXN]; void Dijkstra(typec cost[][MAXN],typec lowcost[],int n,int beg) { for(int i=0;i<n;i++) { lowcost[i]=INF; vis[i]=false; pre[i]=-1; } lowcost[beg]=0; for(int j=0;j<n;j++) { int k=-1; int Min=INF; for(int i=0;i<n;i++) if(!vis[i]&&lowcost[i]<Min) { Min=lowcost[i]; k=i; } if(k==-1) break; vis[k]=true; for(int i=0;i<n;i++) if(!vis[i]&&lowcost[k]+cost[k][i]<lowcost[i]) { lowcost[i]=lowcost[k]+cost[k][i]; pre[i]=k; } } }
二、Dijstra+优先队列
将每次选取到达源点最近点的过程用一个优先队列代替,直接出队得到最近点和距离。但要把已经处理过的点涉及到的已经入队的略过不处理。
代码:

/* * 使用优先队列优化Dijkstra算法 * 复杂度O(ElogE) * 注意对vector<Edge>E[MAXN]进行初始化后加边 */ const int INF=0x3f3f3f3f; const int MAXN=1000010; struct qnode { int v; int c; qnode(int _v=0,int _c=0):v(_v),c(_c){} bool operator <(const qnode &r)const { return c>r.c; } }; struct Edge { int v,cost; Edge(int _v=0,int _cost=0):v(_v),cost(_cost){} }; vector<Edge>E[MAXN]; bool vis[MAXN]; int dist[MAXN]; void Dijkstra(int n,int start)//点的编号从1开始 { memset(vis,false,sizeof(vis)); for(int i=1;i<=n;i++) dist[i]=INF; priority_queue<qnode>que; while(!que.empty()) que.pop(); dist[start]=0; que.push(qnode(start,0)); qnode tmp; while(!que.empty()) { tmp=que.top(); que.pop(); int u=tmp.v; if(vis[u]) continue; vis[u]=true; for(int i=0;i<E[u].size();i++) { int v=E[tmp.v][i].v; int cost=E[u][i].cost; if(!vis[v]&&dist[v]>dist[u]+cost) { dist[v]=dist[u]+cost; que.push(qnode(v,dist[v])); } } } } void addedge(int u,int v,int w) { E[u].push_back(Edge(v,w)); }
三、Bellman-Ford算法
Bellman-Ford算法是对每条边进行松弛,重复|V|次,时间复杂度是O(V*E),伪代码如下:
for(i = 0; i < |V|; i++)
for each edge(u, v) ∈ E
RELAX(u, v)
算法简单,但是实际中不被采用,因为存在大量的无效松弛。
代码:

/* * 单源最短路bellman_ford算法,复杂度O(VE) * 可以处理负边权图。 * 可以判断是否存在负环回路。返回true,当且仅当图中不包含从源点可达的负权回路 * vector<Edge>E;先E.clear()初始化,然后加入所有边 * 点的编号从1开始(从0开始简单修改就可以了) */ const int INF=0x3f3f3f3f; const int MAXN=550; int dist[MAXN]; struct Edge { int u,v; int cost; Edge(int _u=0,int _v=0,int _cost=0):u(_u),v(_v),cost(_cost){} }; vector<Edge>E; bool bellman_ford(int start,int n)//点的编号从1开始 { for(int i=1;i<=n;i++)dist[i]=INF; dist[start]=0; for(int i=1;i<n;i++)//最多做n-1次 { bool flag=false; for(int j=0;j<E.size();j++) { int u=E[j].u; int v=E[j].v; int cost=E[j].cost; if(dist[v]>dist[u]+cost) { dist[v]=dist[u]+cost; flag=true; } } if(!flag) return true;//没有负环回路 } for(int j=0;j<E.size();j++) if(dist[E[j].v]>dist[E[j].u]+E[j].cost) return false;//有负环回路 return true;//没有负环回路 }
四、Spfa
Spfa是Bellman-Ford算法利用队列的优化,Bellman-Ford算法存在大量的无效松弛,spfa对它进行改进,对于每个点只松弛与这个点相关的边。
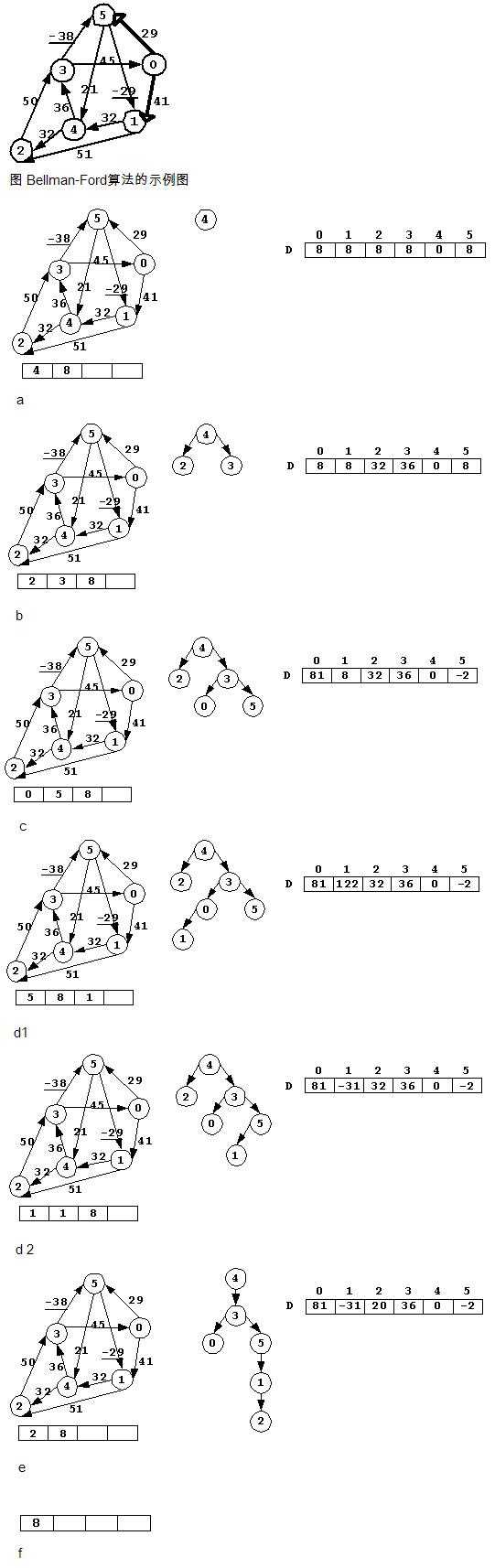
代码:

/* * 单源最短路SPFA * 时间复杂度 0(kE) * 这个是队列实现,有时候改成栈实现会更加快,很容易修改 * 这个复杂度是不定的 */ const int MAXN=1010; const int INF=0x3f3f3f3f; struct Edge { int v; int cost; Edge(int _v=0,int _cost=0):v(_v),cost(_cost){} }; vector<Edge>E[MAXN]; void addedge(int u,int v,int w) { E[u].push_back(Edge(v,w)); } bool vis[MAXN];//在队列标志 int cnt[MAXN];//每个点的入队列次数 int dist[MAXN]; bool SPFA(int start,int n) { memset(vis,false,sizeof(vis)); for(int i=1;i<=n;i++) dist[i]=INF; vis[start]=true; dist[start]=0; queue<int>que; while(!que.empty()) que.pop(); que.push(start); memset(cnt,0,sizeof(cnt)); cnt[start]=1; while(!que.empty()) { int u=que.front(); que.pop(); vis[u]=false; for(int i=0;i<E[u].size();i++) { int v=E[u][i].v; if(dist[v]>dist[u]+E[u][i].cost) { dist[v]=dist[u]+E[u][i].cost; if(!vis[v]) { vis[v]=true; que.push(v); if(++cnt[v]>n) //cnt[i]为入队列次数,用来判定是否存在负环回路 return false; } } } } return true; }
五、Floyd算法
Floyd算法是多源最短路,算法是将每对顶点(i,j)之间的所有其他点都进行松弛。
其状态转移方程如下: map[i,j]=min{map[i,k]+map[k,j],map[i,j]};
代码:

#include<stdio.h> #include<stdlib.h> #define max 1000000000 int d[1000][1000],path[1000][1000]; int main() { int i,j,k,m,n; int x,y,z; scanf("%d%d",&n,&m); for(i=1;i<=n;i++) for(j=1;j<=n;j++){ d[i][j]=max; path[i][j]=j; } for(i=1;i<=m;i++) { scanf("%d%d%d",&x,&y,&z); d[x][y]=z; d[y][x]=z; } for(k=1;k<=n;k++) for(i=1;i<=n;i++) for(j=1;j<=n;j++) { if(d[i][k]+d[k][j]<d[i][j]){ d[i][j]=d[i][k]+d[k][j]; path[i][j]=path[i][k]; } } for(i=1;i<=n;i++) for(j=1;j<=i;j++) if (i!=j) printf("%d->%d:%d\n",i,j,d[i][j]); int f,en; scanf("%d%d",&f,&en); while (f!=en){ printf("%d->",f); f=path[f][en]; } printf("%d\n",en); return 0; }
标签:
原文地址:http://www.cnblogs.com/vwqv/p/5910297.html