机器学习基石(2)--Learning to Answer Yes/No

标签：

本节课主要讲述机器学习怎么解决是非题。

介绍系列课程的第一个模型：perceptron（感知器）

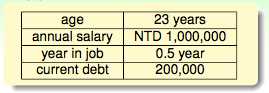
把每一个sample的各种feature用一个向量来表示，也就是下图的x，以上图为例，x₁=age, x₂=annual salary, x₃=year in job, x₄=current detb，也就是说在这里，x是一个四维的向量。

x_i表示维度，w_i表示该维度的重要性。如果一个人（sample）所有的维度和重要性的乘积加起来，如果总分超过了某一个值（threshold），我们决定这个sample可以通过，反之，则要拒绝掉。如果刚好等于threshold，由于几率极小，这里可以忽略。就像抛银币，竖在那里的几率不是没有，只是很小，算来算去有可能还不如瞎猜一个好。得出的结果叫做y，通过用y=+1表示，没有通过用y=–1表示。我们需要找一个模型出来，输入端是各种x，输出端是各种y。这个模型在这里叫做h(x)。

经过数学推导之后得出h(x)：

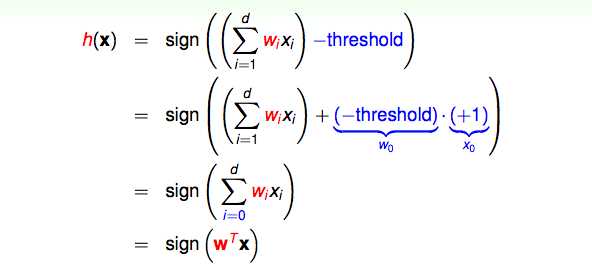
以二维的data为例，h(x)=sign(w₀+w₁x₁+w₂x₂)

features x就是在平面上的点，因为是二维的所以在平面上，这里可以延伸到更高的维度。

labels y就是图中的圈圈或者叉叉。（因为是二元分类）

hypothesis h就是图中把圈圈和叉叉分开的那条线。（在二维空间是线，三维空间是面，更高维度就是超平面）

假设H是平面内所有的线，我们的目标g是在平面内选一条最好的线。没有输入进模型的data先不管，我们先在已经输入进模型的data中找这么一条线能完美的将两种y分开。那么如何找这条线呢？看起来只有先假设一条不完美的线，通过不断的纠错，把它变得完美。

初始的线就设为w₀，然后我们要做的事就是不断的修正w₀直到它达到能够分开两种y的情况。

t是每次修改的次数。

第一步就是识别是否错误，也就是说这条线的符号和y不一致；

第二部就是修正这个错误，将上一个w_t进行修正，并且赋值给w_t+1；

第三部就是重复以上步骤，直到没有错误。就是每一个点都进行验证，如果有错误就进行修正，如果没有错误就对下一个点进行验证，直到所有的点都被验证正确。(cyclic PLA)

初始点的选择是随机的，后续验证的时候对点的选择也可以是随机的。

PLA的最大的缺点是要求data必须是线性可分的。

设想一个很完美的线如下：

wf和wt越来越接近，因为他们的内积越来越大。

PLA在出现错误的时候就会更新，换成数学表示就是两个相乘是异号的。

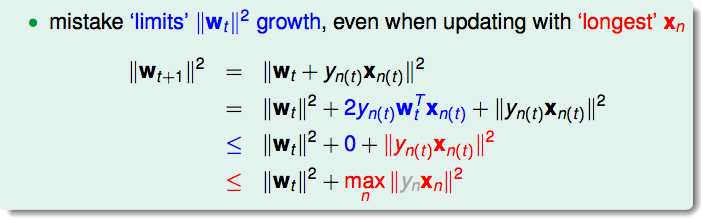
红色部分是w_t和w_t+1的差别，也就是w_t+1在每次犯错之后的变化（成长）。

w_t最多成长x_n的平方。

两个向量的内积在这里只表示他们越来越靠近，并不是因为他们长度的关系。

PLA总结：

优点：简单易用；

缺点：必须线性可分，不知道什么时候能停下来。

更新Flow：增加了噪声对整体数据的干扰的考虑。大部分时候必须对噪声有一定的容忍。

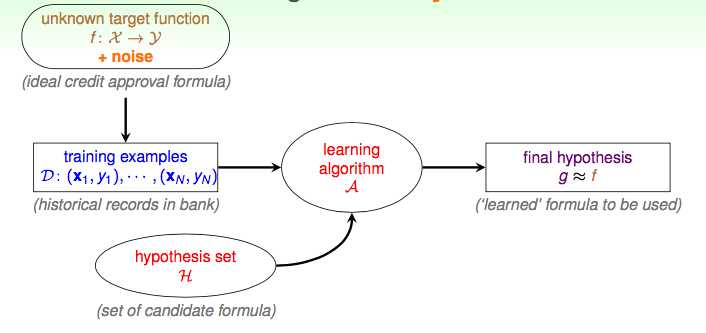
在有噪声的时候，我们的目标从找一条完美的线换成找一条犯错误最少的线。也就是Pocket Algorithm。

先把当前犯错误最少的线装在pocket里，如果我们遇到了更好的线，则替换掉已经在pocket里的线。但是pocket算法比PLA要慢。

手写的数学推导：

总结：

机器学习基石(2)--Learning to Answer Yes/No

标签：

原文地址：http://www.cnblogs.com/cyoutetsu/p/5909908.html