标签:
本节课主要讲在机器学习中,机器如何做到举一反三。

上图可以得出结论,当N超过k的时候,mH的数量会越来越少。对未来成长函数的样子加了一个限制。

mH的数量其实是有一个上限的,这个上限就是关于N的一个多项式。引出定义bonding function B(N,k)

已知上限函数的break point是在k,求这个函数的上限到底是多少。并且,我们不用去管这个函数是什么样子,只需要关注K和N就好了。
bounding function计算表:
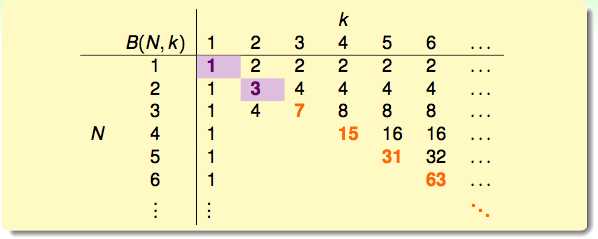
bounding function的几个性质:
1. B(N,1)=1
2. B(N,k)=2N for N>k
3. B(N,k)=2N–1 for N=k
下面要做的就是接触上图中空白的部分,以B(4,3)为例:通过计算得出B(4,3)=11,又可以归纳成(以x4为基准看单双对)2α+β=2N+k
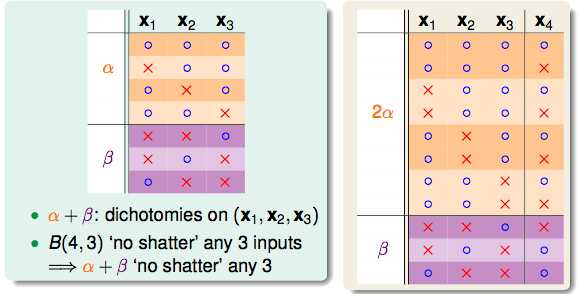
由于任意三个点不能shatter,得出结论α+β≤B(3,3);
在单独的α中,任意两个点不能shatter,得出结论α≤B(3,2);
由此可以得出:

把这个拓展到N和k的情况下:

我们可以得出这个bounding function的上限,也就是这个上限函数的上限是(也就是之前讲过的成长函数的上限也被确定了):
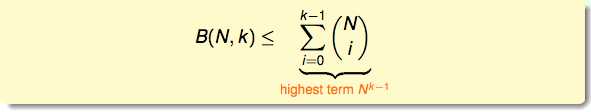
所以可以得出结论:如果k存在的话,B(N,k)的上限确实是一个关于N的多项式。最大值是Nk–1。
有时候我们写不出mH,但是我们可以写出bounding function。
再次返回霍夫丁不等式,我们可以通过一系列数学证明得到如下结果:
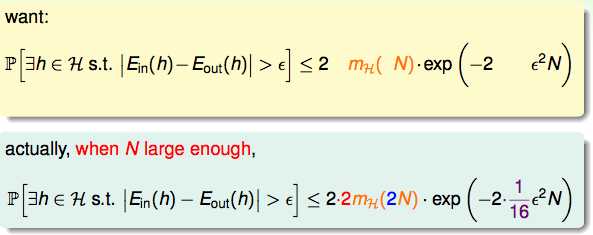
证明的过程不重要,但是证明的技巧在后面可能会被用到:
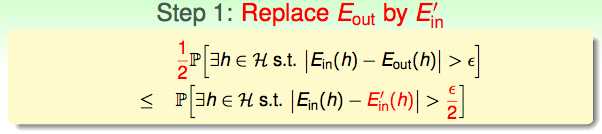
Ein是有限的,但是Eout确实无限的,如果我们假设又从population中取了另一批sample,通过学习这一批sample得出了另一个Ein`,而这个Ein`应该和population中的Eout发生BAD事件的概率是相同的,所以,两批sample发生BAD事件也是相同的,Eout于是从无限就可以替换为有限个了。
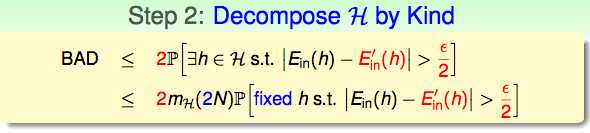
把hypothesis set分类:由于上一步从population中取了另一批的sample,所以N应该由2N来替代。

采用无放回抽样(Hoeffding without Replacement),得到的结果也是一样的。
最后得出结果(发生BAD事件的概率):

总结:

机器学习基石(6)--Theory of Generalization
标签:
原文地址:http://www.cnblogs.com/cyoutetsu/p/5912531.html