标签:
书上有的内容我就不重复赘述了,只需要将部分重要的知识点归纳总结一下。
1.进制
2.字
3.字节顺序
4.布尔代数
5.整数表示
6.补码
-补码是最常见的有符号数的计算机表示方式。
7.无符号数与有符号数转换
强制类型转换的结果保持位值不变,改变解释这些位的方式。 处理同样字长的有、无符号数之间相互转换的规则:数值可能会变,但是位模式不变。(底层的位表示保持不变)
8.扩展数字的位表示
9.截断数字
可能会改变数值——溢出的一种形式。
对于无符号数字x,截断到k位,相当于计算:x mod 2(k)。(k次幂)
10.整数运算
11.浮点数:
标准:IEEE标准754
(1)二进制小数 定点表示法:“.”为界(不能有效的表示很大的数)
十进制:小数点左边的数字的权是10的非负幂,得到整数值;右边的数字的权是10的负幂,得到小数值。 二进制:小数点左边的数字的权是2的非负幂,右边的数字的权是2的负幂。
(2)IEEE浮点表示
符号:s决定这个数是负数(s = 1)还是正数(s = 0),而对于数值0的符号位解释作为特殊情况处理。
尾数:M是一个二进制小数,它的范围是1 ~ 2-ε,或者是0 ~ 1-ε。
阶码:E的作用是对浮点数据加权,这个权重是2的E次幂(可能是负数)。
一个单独的符号位s直接编码符号s。
k位的阶码字段exp = ek-1…e1e0编码阶码E。
n位小数字段frac = fn-1…f1f0编码尾数M,但是编码出来的值也依赖于阶码字段的值是否等于0。
在float中,s、exp和frac字段分别为1位、k = 8 位和n = 23位,得到一个32位的表示;
在double中,s、exp和frac字段分别为1位、k = 11 位和n = 52位,得到一个64位的表示。
1.从逆向角度考虑为什么无符号数、有符号数(2进制补码)、浮点数之间的转换会产生漏洞?
任何漏洞产生都必然因为系统不可更改的局限性——>无符号数、有符号数、浮点数的局限性——>无符号数或者有符号数的表示范围有限,而浮点数虽然编码范围大,但是不精确。
2.怎么样让负数等于正数?
在负数x后加上U,可以使其转换为(2^w+x)
3.整数与浮点数表示同一个数字的关系?
整数与浮点数表示同一个数字时,化成二进制形式之后,可以看到,整数等于1 的最高有效位之后的数字,与浮点数小数部分的高位是相匹配的
4.当阶码全为1、小数域全为0时,得到的值表示无穷;当阶码全为1、小数域不全为0时,结果是NaN(not a number)
5.整数与浮点数转换规则?
整数->浮点数:整数转换成二进制表示,然后小数点左移若干位得到规格化表示;取出小数部分的数值,在后面补0使其达到23位; 用frac加上偏置量得到的结果用二进制表示,放在取出的部分前面,再加上一个符号位即可。
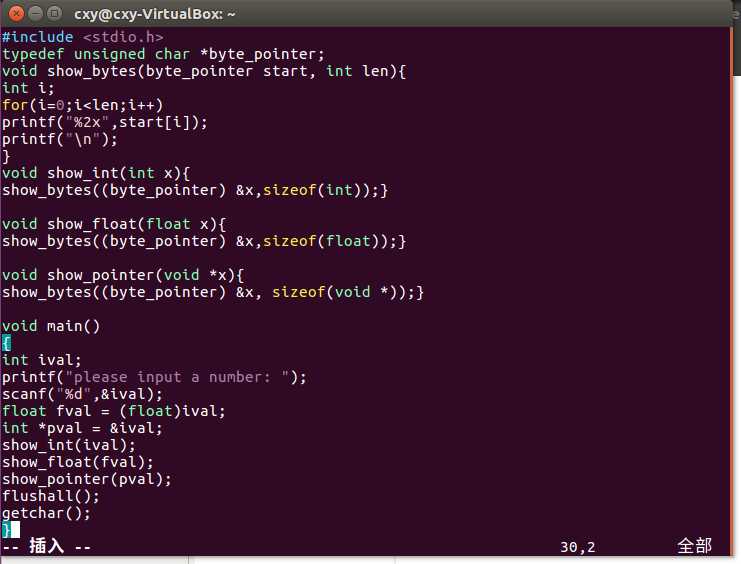
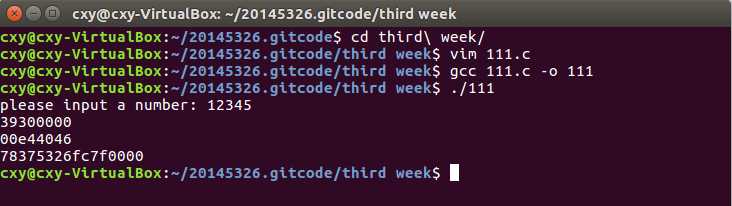
p28的代码我加了个main()函数
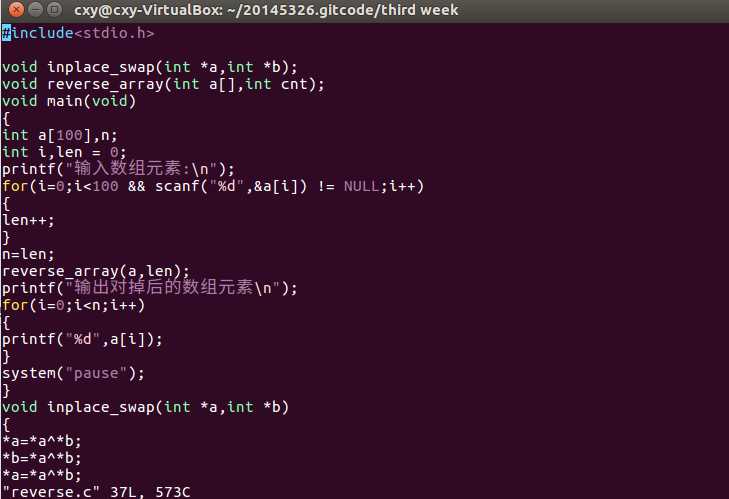
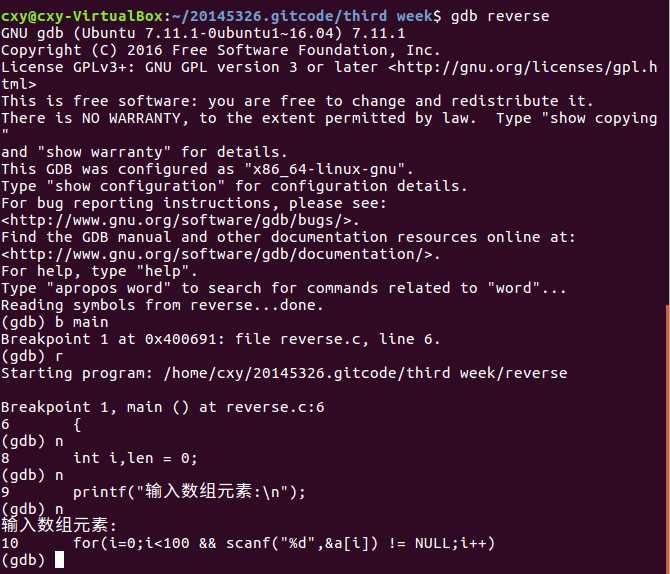
p35的代码用gdb调试练习:
p44的代码运行:
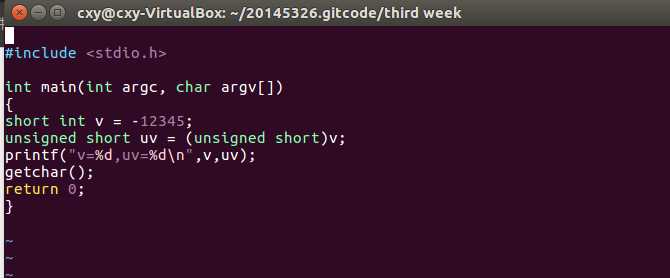
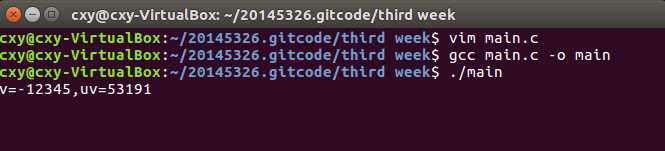
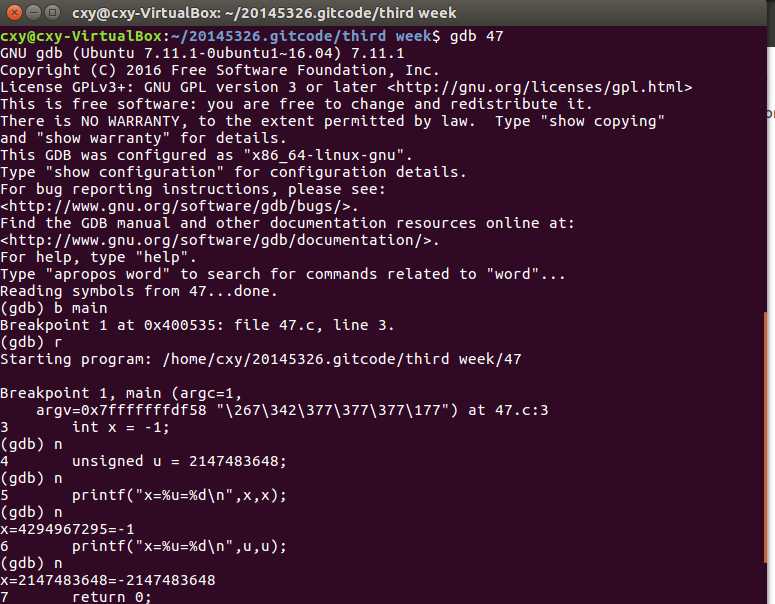
p47的代码编译及gdb调试:

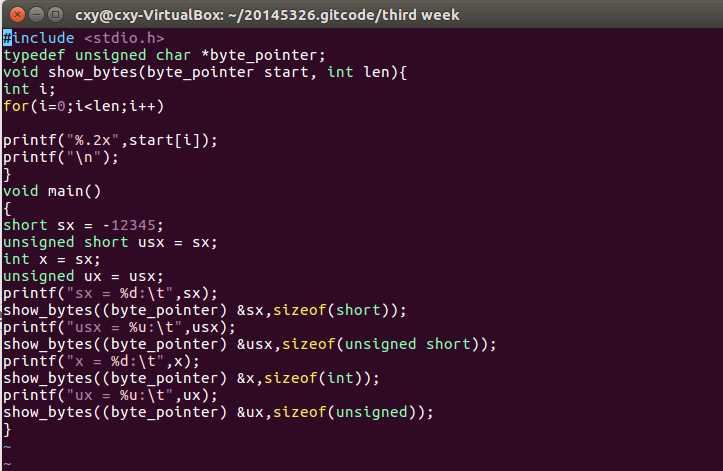
p49的代码编译练习:
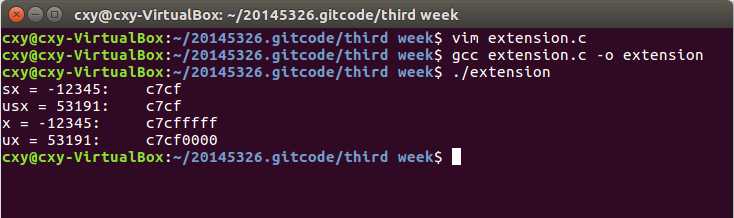
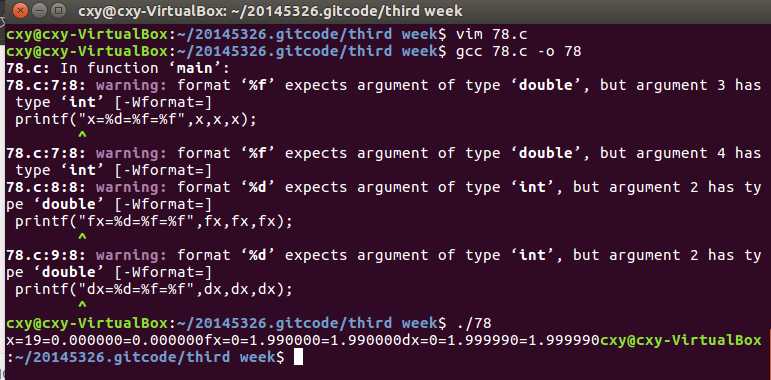
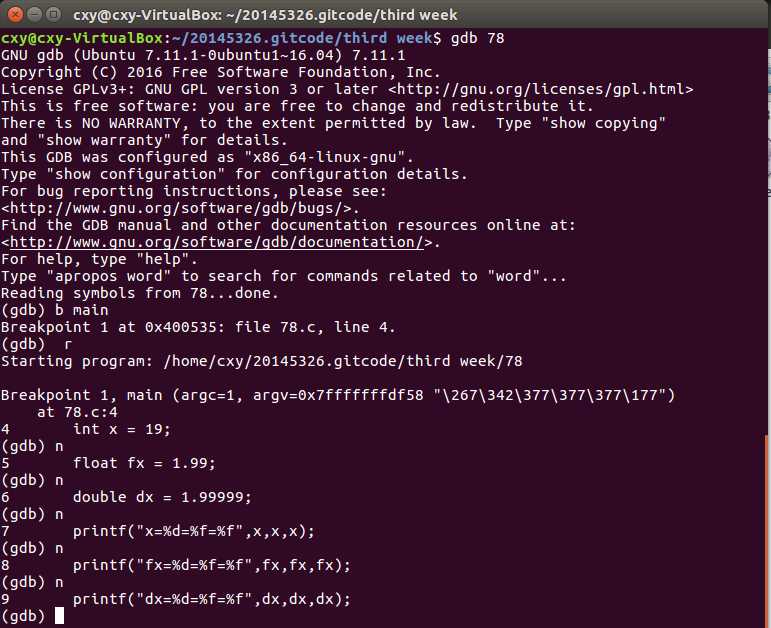
p78的代码编译及练习:
家庭作业
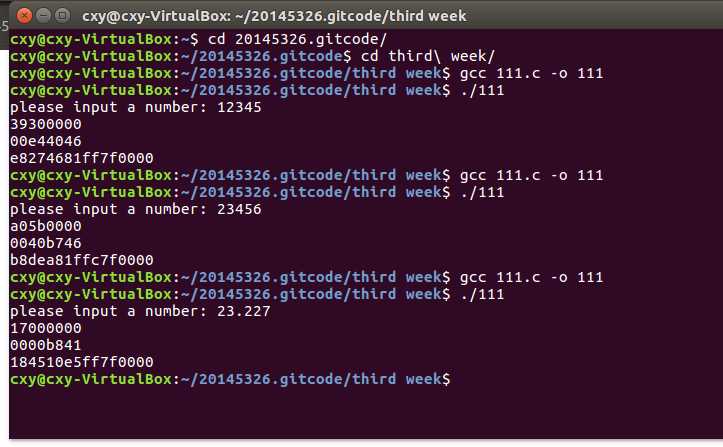
2.56 用不同示例值运行P28代码
2.59
(x&0xFF) | (y&~0xFF)
2.61
A. !~x
B. !x
C. !~(x>>((sizeof(int)-1)<<3))
D. !(x&0xFF)
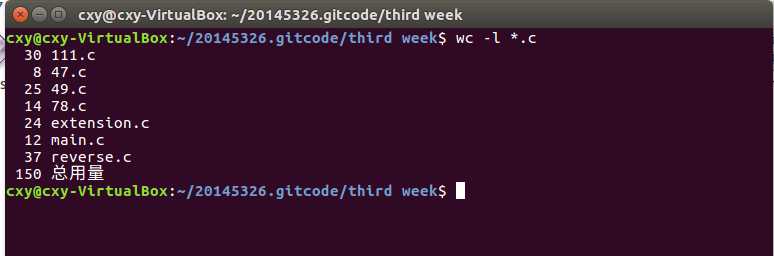
本周所敲代码行数:
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/2 | 20/20 | |
| 第二周 | 58/58 | 1/3 | 20/40 | |
| 第三周 | 150/208 | 1/4 | 22/62 |
20145326蔡馨熠《信息安全系统设计基础》第三周学习总结
标签:
原文地址:http://www.cnblogs.com/cxy1616/p/5926435.html