标签:
1.定义
堆:若将此序列所存储的向量R[1..n]看做是一棵完全二叉树的存储结构,则堆实质上是满足如下性质的完全二叉树
树中任一非叶子结点的关键字均不大于(或不小于)其子结点的关键字。分为大根数(默认)和小根树(自定义cmp)
摘取:http://blog.csdn.net/blade2001/article/details/6901100
STL里面的堆操作一般用到的只有4个。
make_heap();、pop_heap();、push_heap();、sort_heap();
他们的头函数是algorithm
首先是make_heap();
他的函数原型是:
void make_heap(first_pointer,end_pointer,compare_function);
一个参数是数组或向量的头指针,第二个向量是尾指针。第三个参数是比较函数的名字
。在缺省的时候,默认是大跟堆。(下面的参数都一样就不解释了)
作用:把这一段的数组或向量做成一个堆的结构。范围是(first,last)
然后是pop_heap();
它的函数原型是:
void pop_heap(first_pointer,end_pointer,compare_function);
作用:pop_heap()不是真的把最大(最小)的元素从堆中弹出来。而是重新排序堆。它
把first和last交换,然后将[first,last-1)的数据再做成一个堆。
接着是push_heap()
void pushheap(first_pointer,end_pointer,compare_function);
作用:push_heap()假设由[first,last-1)是一个有效的堆,然后,再把堆中的新元素加
进来,做成一个堆。
最后是sort_heap()
void sort_heap(first_pointer,end_pointer,compare_function);
作用是sort_heap对[first,last)中的序列进行排序。它假设这个序列是有效堆。(当然
,经过排序之后就不是一个有效堆了)
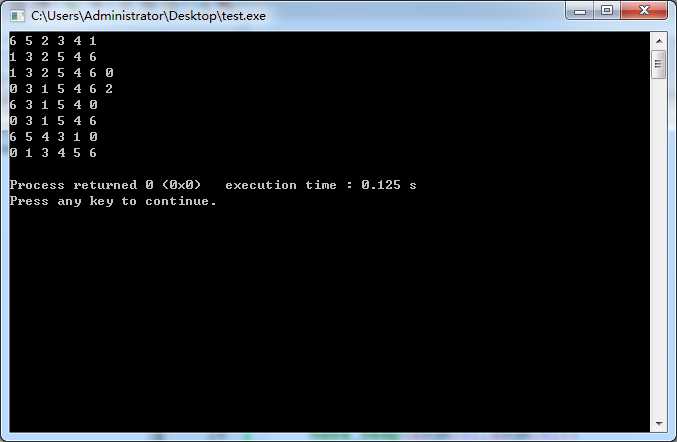
1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 int num[10]= {6,3,2,5,4,1}; 5 void print(int len) 6 { 7 for(int i=0; i<len; i++) 8 cout<<num[i]<<" "; 9 cout<<endl; 10 } 11 bool cmp(int a,int b) 12 { 13 return a>b; 14 } 15 int main() 16 { 17 //*make_heap() 18 make_heap(&num[0],&num[6]); 19 print(6); 20 make_heap(&num[0],&num[6],cmp); 21 print(6); 22 //*push_heap() 23 num[6]=0; 24 push_heap(&num[0],&num[7]); 25 print(7); 26 push_heap(&num[0],&num[7],cmp); 27 print(7); 28 29 30 //*pop_heap 31 pop_heap(&num[0],&num[6]); 32 print(6); 33 pop_heap(&num[0],&num[6],cmp); 34 print(6); 35 //*sort_heap 36 sort_heap(&num[0],&num[6],cmp); 37 print(6); 38 sort_heap(&num[0],&num[6]); 39 print(6); 40 41 42 }
标签:
原文地址:http://www.cnblogs.com/sxy-798013203/p/5928973.html