标签:
摘要: 标量滤波的过程分析和证明及C实现,希望能够帮助入门的小白,同时得到各位高手的指教。并不涉及其他Kalman滤波方法。
本文主要参考自《A Introduction to the Kalman》 (需要的同学可以自行百度,也可以找到中文版的)
注:递归思想,高斯分布独立性的应用,数据融合的应用
一,什么是Kalman 滤波(已经了解的同学可以跳过这里)
卡尔曼在博士期间发表了用递归方法解决离散数据线性滤波 问题的论文(关于Kalman 滤波的真正第一人还是有待探讨的,有兴趣的同学自行查找)。从此以后,Kalman滤波器得到了广泛的应用,比如自主导航的姿态解算(四轴飞行器也有部分开发商使用了Kalman滤波,但是人家用到不是今天讲的标量滤波,有时间可以探讨下)
其实Kalman滤波器由5条递归的数学公式表示。5条公式提供十分有效的计算方法,描述了系统状态的变化(其实就是观测量的变化,后续涉及系统状态请自行对应),能得到与真实值最小误差的估计(这个估计可以当作真实值使用)。这5条公式,可以做到估计过去,现在,甚至未来的系统状态,而不用当心系统状态的变化模型。
同时Kalman也是提出结合状态空间和测量空间的滤波方法。而Wiener滤波则是仅在测量空间上滤波。Wiener滤波需要知道所有[0,n-1]时刻协方差的先验知识,Kalman直接可以通过上一时刻即n-1时刻的状态信息和均方误差信息就可递推得到n时刻的估计,其实也是利用了[0,n-1]时刻的先验知识。
二,什么样的数据适合于Kalman 滤波
可以先明确的指出的是:
三,Kalman 滤波的数学推导及物理意义:
3.1背景(这里举经典的例子):
假设我们要研究的对象是一个房间的温度。根据你的经验判断,这个房间的温度是恒定的, 也就是现在这一分钟的温度等于过去一分钟的温度(假设我们用一分钟来做时间单位)(先验估计) 。假设你对你的经验不是 100% 的相信,可能会有上下偏差几度。我们把这些偏差看成是高斯白噪声,也就是这些偏差跟前后时间是没有关系的而且符合高斯分布。
另外,我们在房间里放一个温度计,但是这个温度计也不准确的, 测量值和实际值有偏差。我们也把这些偏差看成是高斯白噪声。
好了, 现在对于某一分钟我们有两个有关于该房间的温度值: 你根据经验的预测值 (系统的 预测值)和温度计的值(测量值)。
Kalman要解决的问题是如何使用这两个值结合他们各自的噪声来估算出房间的实际温度值。
假如我们要估算 k 时刻的是实际温度值。 首先你要根据 k-1 时刻的温度值, 来预测 k 时刻的 温度。因为你假定温度是恒定的(就算事实不是恒定的也没有关系,因为你不相信你这个假定),所以你会得到 k 时刻的温度预测值是跟 k-1 时刻一样的, 假设是 23 度,同时假设该估计值的高斯噪声的标准差是 5 度(这里为何是5,首先假设预测噪声标准差是4,上次最优估计误差为3,求平方和即得。至于为何是平方和,可以看做两个高斯过程相加[上次最优估计结果是个高斯过程,这次预测也是高斯过程],所得的也是高斯过程,方差为原先两者的方差之和)。
然后,你从温度计那里得到了 k 时刻的温度值,假设是 25 度,同时该值的噪声标准差是 4 度。 由于我们用于估算 k 时刻的实际温度有两个温度值, 分别是 23 度和 25 度。 究竟实际温度是多少呢?相信自己还是相信温度计呢?究竟相信谁多一点, 我们可以上次的估计值的噪声方差及上次的最优估计方差总和之比判断。算出比例因子Kg: Kg^2=5^2/(5^2+4^2) ,所以 Kg=0.78 ,我们可以估算出 k 时刻的实际温度值(最优估计)是: 23+0.78*(25-23)=24.56 度[估计值+Kg*(测量值-估计值)]。可以看出, 所以估算出的最优温度值偏向温度计的值。 现在我们已经得到 k 时刻的最优温度值了,下一步就是要进入 k+1 时刻,进行新的最优估算。到现在为止,好像还没看到什么递归的东西出现。对了,在进入 k+1 时刻之前,我 们还要算出 k 时刻那个最优值( 24.56 度)的噪声标准差。算法如下:
((1-Kg)*5^2)^0.5=2.35 。这里 的 5 就是上面的k 时刻你预测的那个 23 度温度值的标准差,得出的 2.35 就是进入 k+1 时刻以 后 k 时刻估算出的最优温度值的标准(对应于上面的 3 ) 。 就是这样,卡尔曼滤波器就不断递归,从而估算出最优的温度值。他运行的 很快, 而且它只保留了上一时刻的 最优估计误差标准差。 上面的Kg , 就是卡尔曼增益 ( Kalman Gain ) 。 他可以随不同的时刻而改变他自己的值,是不是很神奇!
三,Kalman 滤波的过程分析
这里引用了《An Introduction to Kalman》
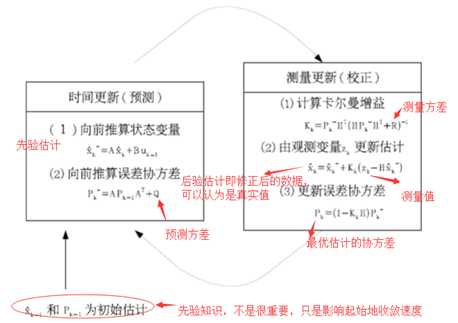
这里稍微解释下最优估计的协方差(误差协方差):为何要称作协方差呢,一开始认为协方差明明是两个变量间的。可以留意预测公式2和校正公式3(公式3目前可能看不出来),根据实例中讲到的两个高斯分布相乘,可以理解为这是上一次最优估计和当前预测值(从时间上看是两个变量)的协方差。
四.Kalman 的证明及物理意义
上面图片看不懂没关系,明白各个物理量就可以了,说实话一维的应用会在上面再修改一下。
证明:
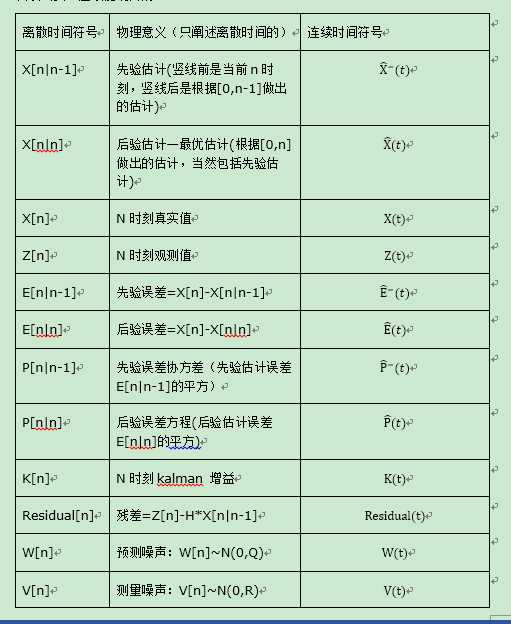
几个假设和模型
即等于上个时刻的“真实值”+控制量+误差(W[n]~N(0,Q))。
因此,给出先验估计X[n|n-1]= A*X[n-1|n-1]+B*U(n);
即等于真实值得数乘+误差(V[n]~N(0,R))
给出采用下面的修正公式:X[n|n]=X[n|n-1]+K[n]*Residul[n]。
所以问题只剩下如何找到合适的K[n]使得估计最优,即后验误差协方差P[n|n]最小(越小说明越接近真实值X[n])
即在连续时间下,后验误差协方差Pt 满足:
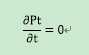
这里推广到联系时间下证明,只是为了方便求极值,结论可以在离散时间适应。




Kalman 过程详解:
(1) 预测:做出先验估计x[n|n-1]=A*x[n-1|n-1];
【对于一维的情况,A可以看成一个常数使用,经常取1,同时对于B经常取零(---可能有人会有疑问:取0没事吗,可以放心的告诉你,问题不大。反过来想想,这只是一个估计,可以在估计噪声方差得到修正)】
(2) 向前推算协方差:做出预测后的新的概率分布的方差(预测上次的最优估计为当前时刻的先验估计这个过程可以当成一个符合预测过程噪声分布的和另一个(上一次的最优估计可以看做高斯分布的)也符合高斯分布的相加。预测结果也是符合高斯噪声分布的,方差是两个相互独立的方差之和)。
【对于一维的情况,P[n|n-1]=P[n-1|n-1]+Q。 Q为预测方差,代表对预测的不信任程度,工程上根据实际调节以改善滤波器的性能:动态效果和去噪效果】
(3) 计算卡尔曼增益:
【对于一维的情况,K[n]=H*P[n|n-1]/{H^2*P[n|n-1]+R}。其中H是对观测的响应倍数,通常取1,R为测量的方差,工程上一般都可以直接获得】
(4) 更估计值:做出后验估计,修正后的估计值,更接近真实值。
【对于一维的情况,最优估计由下式给出:
x[n|n]=x[n|n-1]+K[n]*{z[n]-x[n|n-1]}。其中z[n]为观测值】
(5) 更新误差协方差:得到最优估计的概率分布的方差。
【对于一维的情况,新的误差协方差由下式给出:
P[n|n]=(1-K[n]*H)*P[n|n-1]】
#include "Kalman.h" /** *@function: - 卡尔曼滤波器初始化 *@kalmanFilter:卡尔曼滤波器结构体 *@init_x:待测量的初始值 *@init_p:后验状态估计值误差的方差的初始值 */ void kalmanFilter_init(KalmanStructTypedef *kalmanFilter, float init_x, float init_p,float predict_q,float newMeasured_q) { kalmanFilter->x = init_x;//待测量的初始值,如有中值一般设成中值 kalmanFilter->p = init_p;//后验状态估计值误差的方差的初始值(不要为0问题不大) kalmanFilter->A = 1; kalmanFilter->H = 1; kalmanFilter->q = predict_q;//预测(过程)噪声方差 影响收敛速率,可以根据实际需求给出 kalmanFilter->r = newMeasured_q;//测量(观测)噪声方差 可以通过实验手段获得 } /** *@function: - 卡尔曼滤波器 *@kalmanFilter:卡尔曼结构体 *@newMeasured;测量值 *返回滤波后的值 */ float kalmanFilter_filter(KalmanStructTypedef *kalmanFilter, float newMeasured) { /* Predict */ kalmanFilter->x = kalmanFilter->A * kalmanFilter->x;//%x的先验估计由上一个时间点的后验估计值和输入信息给出 kalmanFilter->p = kalmanFilter->A * kalmanFilter->A * kalmanFilter->p + kalmanFilter->q; /*计算先验均方差 p(n|n-1)=A^2*p(n-1|n-1)+q */ /* Correct */ kalmanFilter->gain = kalmanFilter->p * kalmanFilter->H / (kalmanFilter->p * kalmanFilter->H * kalmanFilter->H + kalmanFilter->r); kalmanFilter->x = kalmanFilter->x + kalmanFilter->gain * (newMeasured - kalmanFilter->H * kalmanFilter->x);//利用残余的信息改善对x(t)的估计,给出后验估计,这个值也就是输出 kalmanFilter->p = (1 - kalmanFilter->gain * kalmanFilter->H) * kalmanFilter->p;//%计算后验均方差 return kalmanFilter->x; }
#ifndef _Kalman_H_ #define _Kalman_H_ //标量卡尔曼滤波 typedef struct { float x; // 系统的状态量 float A; // x(n)=A*x(n-1)+u(n),u(n)~N(0,q) float H; // z(n)=H*x(n)+w(n),w(n)~N(0,r) float q; // 预测过程噪声协方差 float r; // 测量过程噪声协方差 float p; // 估计误差协方差 float gain;//卡尔曼增益 }KalmanStructTypedef; void kalmanFilter_init(KalmanStructTypedef *kalmanFilter, float init_x, float init_p,float predict_q,float newMeasured_q); float kalmanFilter_filter(KalmanStructTypedef *kalmanFilter, float newMeasured); #endif
标签:
原文地址:http://www.cnblogs.com/guiguzhixing/p/5930003.html