标签:
1~~特点:用一维数组来描述线性表,用游标代替指针指示节点在数组中的相对位置。不设“指针”类型的高级语言中适用链表结构。
2~~线性表的静态链式存储结构
//
// 静态单链表.h
// 单链表的静态存储
//
// 6 // Copyright (c) 2014年 dashuai. All rights reserved.
//
#ifndef SLIST_H
#define SLIST_H
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
typedef struct{
int data;//数据域
int cur;//指示下一个元素在数据你的下标,相当于指针
} Component, SLinkList[MAXSIZE];
//初始化静态链(整个数组空间)
void initSlist(SLinkList *L);
// 分配静态链表的结点
int mallocSNode(SLinkList *L);
//释放下表为 n 的结点
//其实这里是模拟了动态链表的动态内存分配和释放,库函数 malloc 和 free
void freeSNode(SLinkList *L, int n);
#endif
//这是实现它
#include "SList.h" //初始化静态链(整个数组空间) void initSlist(SLinkList *L) { //创建一个备用链表,存储没有呗使用的结点或者被删除的结点 //否则,因为是静态的数组形式,总是插入或者删除,会出现假满假空的现象 for (int i = 0; i < MAXSIZE - 1; i++) { L[i]->cur = i + 1; } L[MAXSIZE - 1]->cur = 0;//尾结点游标=0,指示是尾结点 for (int i = 0; i < MAXSIZE; i++) { printf("打印现在的结点data=%d, cur=%d: \n", L[i]->data, L[i]->cur); } } /* 因为main 函数里的空闲链表没有初始化,导致内部结构成员有垃圾值 */ // 分配静态链表的结点,从备用链表里取出 int mallocSNode(SLinkList *L) { //指针 i 存储的结点的后继地址 int i = L[0]->cur; printf("i = %d\n", i); //模拟的动态内存分配过程 if (i) { //游标后移一个结点单元,指向当前指向结点的下一个结点 // cur 指向下一结点 L[0]->cur = L[i]->cur; } return i; } //释放表 data 为 n 的结点,其实是回收到了备用链表里 //其实这里是模拟了动态链表的动态内存分配和释放,库函数 malloc 和 free void freeSNode(SLinkList *L, int n) { //把结点n连接到备用链表上的过程,完全模拟的动态链表,但是其实不是动态的 //当前结点 n,指向备用链表头结点的后继 L[n]->cur = L[0]->cur; //头结点指向这个当前回收结点 n,以后每次回收,都依次头插 L[0]->cur = n; //显然是头插法 }
二、循环链表
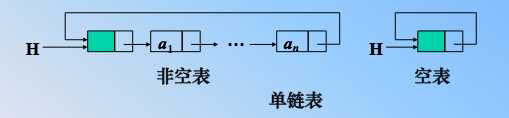
所谓循环,就是到尾结点,没有空指针,尾结点反而指向了头结点,成环,说白了,就是尼玛头尾张一起了。那么从环中的任意一个结点都能达到表里其他结点,可以循环单恋,也可以多重链起来,俗话说的好,掌握好了单链表的思想和存储,那么一切都是变化罢了,思想没有变。操作大概一样。
差别:
1、循环条件变了,没有空指针,那么循环遍历的终止条件就是看尾指针指向头结点的时候
2、对于循环单链表,又有演化:
如果是头指针表示的循环单链,那么找最后一个元素时间复杂度是 o(n),不过,如果是尾指针表示的,那么找第一个元素是 p->next->next,找最后一个元素是 p 就行了,时间复杂度才是0(1)。
比如:要求合并两个循环单链表A 和 A,该怎么做?
因为是循环的,链表,那么只需要操作两个指针就行,时间复杂度为 o(1)
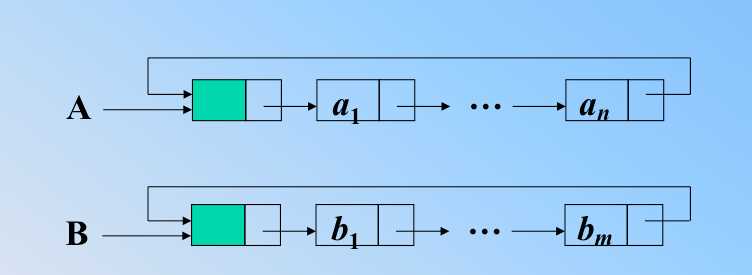
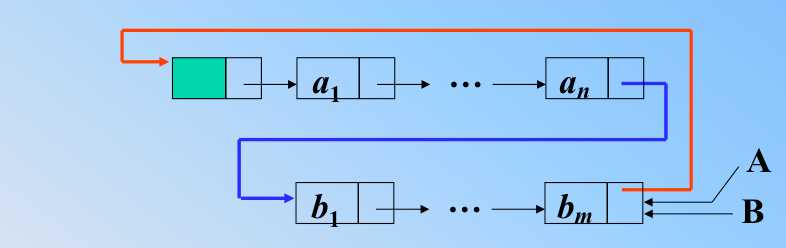
//此图时间复杂度不是1,应该在这里体现尾指针的方便,需要让两个表的头指针分别变味尾指针,才是操作两个指针(假设是尾指针)
//指针 c 指向 A 表的头结点 c = a->next; //A 表的尾指针 指向 B 表的首元素,注意不是头结点 a->next = b->next->next; //B 表的尾指针指向 c b->next = c; //最后指针合并 a = b;
三、双链表和循环
单链表的结点,有指示后继的指针域→,找后继结点方便;查找某结点的后继结点的执行时间为O(1)。 没有指示前驱的指针域→,找前驱结点难,从表头出发查找。 即:查找某结点的前驱结点的执行时间为O(n)。这时候双链表应运而生!
双向链表:在单链表的每个结点里再增加一个指向其直接前驱的指针prior ,这样链表中就形成了有两个方向不同的链,故称为双向链表。
存储结构:
1 typedef struct node{ 2 int data; 3 struct node *prior; 4 struct node *next; 5 } node, *doubleLinklist;
双向链表也可以有循环,让头结点的前驱指针指向链表的最后一个结点,让最后一个结点的后继指针指向头结点。 这里需要注意一下空的双向循环链表的表示:
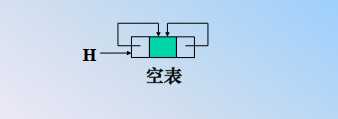
俗话就是自己干自己的情形,说明是空表,只有一个孤单的头结点
双向链表还要一个特点:对称性,比如结点 P,那么存在如下语句
p->prior-next = p;
p->next->prior = p;
双向链表,有些操作 (如:ListLength、GetElem等) ,仅涉及一个方向的指针,算法与线性链表的相同。但插入、删除,则需同时修改两个方向上的指针。这是双向链表的一个难点。
还是用循环双向链表举例:c 99新特性 bool 类型,需要使用#include <stdbool.h>,还有随用虽定义的变量,很爽了,和 c++兼容性越来越强!
//初始化双向循环链表 //指向指针的指针和返回指针类型,手动分配内存是堆,不是栈,return 栈的内存是错误的,return 堆 么问题! void initDoubleCircleLinklist(doubleLinklist *L) { //l 是头指针 //这里标准的写法是这样(林锐语),因为 l 是指针类型,不是不尔类型也不是整型(c 99后来也有了布尔) if (NULL == *L) { *L = (doubleLinklist)malloc(sizeof(node));//头指针指向头结点 //开始是空, (*L)->next = *L; (*L)->prior = *L; } } //求长度 int lengthDoubleCircleLinklist(doubleLinklist L) { //默认表已经存在 int iNum = 0; doubleLinklist p = L; while (p->next != L) { p = p->next; iNum++; } return iNum; } //判空操作 //c99新增bool,为了提高 和c++兼容性 bool isEmpty(doubleLinklist L) { return (L->prior == L) && (L->next == L) ? 1 : 0; } //找到元素 i 的前驱,并用指针反悔 doubleLinklist getIElem(doubleLinklist L, int i) { doubleLinklist p = L; for (int j = 1; j < i; j++) { p = p->next; } return p; } //在循环双链表的第 i 个位置插入一个元素, void insertNode(doubleLinklist L, int i, int nodeElem) { doubleLinklist p = NULL; //先判断合法性 if (i > 0 && i <= lengthDoubleCircleLinklist(L) + 1) { //找到 i 的前驱,后继也可以 p = getIElem(L, i); //新建结点 doubleLinklist s = (doubleLinklist)malloc(sizeof(node)); s->data = nodeElem; //搞定无指针的那一端,不能中途断链,然后再搞另一端 s->next = p->next; p->next->prior = s; p->next = s; s->prior = p; } } //删除第 i 个元素,并把删除的元素值保存 void deleteNode(doubleLinklist L, int i, int *rec) { doubleLinklist p = NULL; if (!(i < 1 || i > lengthDoubleCircleLinklist(L) + 1)) { p = getIElem(L, i); p = p->next; //删除结点 *rec = p->data; p->prior->next = p->next; p->next->prior = p->prior; //释放内存,p 指向的内存区域清空,但是 p 没变 free(p); //杜绝野指针 p = NULL; } else { puts("错误!无法删除"); } } //遍历(正) void traverseLinklist(doubleLinklist L) { doubleLinklist p = L->next; for (int i = 0; i < lengthDoubleCircleLinklist(L); i++) { printf("%d \t", p->data); p = p->next; } putchar(‘\n‘); } //遍历(反)一个意思 //销毁 void destoryDoubleCircleLinklist(doubleLinklist L) { //一个一个的依次释放,需要两个指示指针 doubleLinklist p = NULL; doubleLinklist q = NULL; q = L->next; p = q; //p = q = L; while (q != L) { q = q->next; free(p); p = q; } free(L); L = NULL; } #endif /* defined(____________circualLInked__) */
最重要的就是插入和删除算法!插入和删除两者的操作关键前提步骤就是获得操作对象的前驱的那一步,而表长为 n 的话,那么时间复杂度均为 O(n)。
// // main.c // Copyright (c) dashuai. All rights reserved. // #include "circualLInked.h" int main(int argc, const char * argv[]) { //建表 puts("建循环双向链表"); doubleLinklist L; initDoubleCircleLinklist(&L); //判空 puts("循环双向链表初始化之后是空表么?"); if (isEmpty(L)){ puts("表是空的"); } else { puts("表不空"); } puts("循环双向链表的表长?"); printf("%d \n", lengthDoubleCircleLinklist(L)); puts("插入一些结点"); //最好不要硬编码 for (int i = 0; i < 5; i++) { insertNode(L, i + 1, i); //0 1 2 3 4 } //判空 puts("循环双向链表插入之后是空表么?"); if (isEmpty(L)){ puts("表是空的"); } else { puts("表不空"); } //头结点不算 puts("循环双向链表的表长?"); printf("%d \n", lengthDoubleCircleLinklist(L)); //遍历一下看看 puts("遍历(正向)循环双向链表"); traverseLinklist(L); //删除第二个元素 puts("删除第二个结点,1"); int receive = 0; deleteNode(L, 2, &receive); printf("%d \n", receive); //遍历一下看看 puts("遍历(正向)循环双向链表"); traverseLinklist(L); //销毁 puts("销毁循环双向链表"); destoryDoubleCircleLinklist(L); return 0; }
建循环双向链表
循环双向链表初始化之后是空表么?
表是空的
循环双向链表的表长?
0
插入一些结点
循环双向链表插入之后是空表么?
表不空
循环双向链表的表长?
5
遍历(正向)循环双向链表
0 1 2 3 4
删除第二个结点,1
1
遍历(正向)循环双向链表
0 2 3 4
销毁循环双向链表
Program ended with exit code: 0
小结:关键字:顺序、链式,静态、动态
1、顺序存储特点:
逻辑顺序与物理顺序一致,本质上是用数组存储线性表的各个元素(即随机存取);存储密度大,存储空间利用率高,可以任意访问任意结点。但是插入删除不方便,需要移动大量元素。是时间换取空间。
2、链式存储特点:
元素之间关系采用元素所在的节点的”指针”信息表示(插、删不需要移动节点)。结点空间可以动态申请和释放,数据元素的逻辑次序靠结点的指针来指示,插入 和删除时不需要移动数据元素。链式存储结构的缺点:每个结点的指针域需额外占用存储空间。当数据域所字节不多时,指针域所占存储空间的比重显得很大。链表 是非随机存取结构。对任一结点的操作都要从头指针依链查找该结点,这增加了算法的复杂度。不便于在表尾插入元素:需遍历整个表才能找到位置。 链表插入、 删除运算的快捷是以空间代价来换取时间。
3、静态存储特点:
在程序运行的过程中不用考虑追加内存的分配问题。
4、动态存储特点:
可动态分配内存,有效利用内存资源,使程序具有可扩展性。
线性表逻辑结构特点:只有一个首结点和尾结点;除首尾结点外其他结点只有一个直接前驱和一个直接后继。线性结构的逻辑关系是一对一(1:1)的。
标签:
原文地址:http://www.cnblogs.com/xiaoyoucai/p/5932342.html