标签:
大家好久不见,实战部分一直托更,很不好意思。本文实验数据与代码来自机器学习实战这本书,倾删。
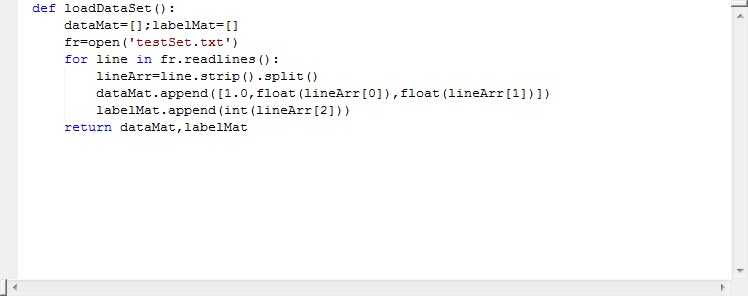
还是一样,设置两个数组,前两个作为特征值,后一个作为标签。当然这是简单的处理,实际开发中特征值都是让我们自己选的,所以有时候对业务逻辑的理解还是很重要的。
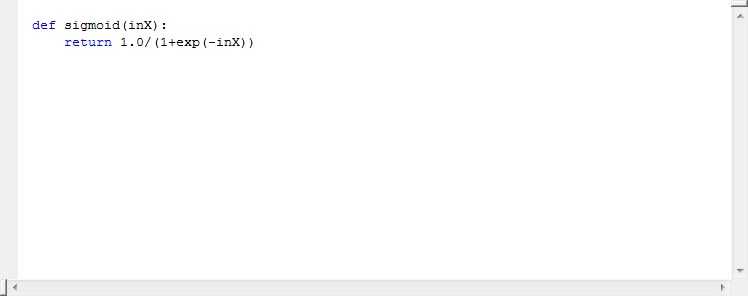
这段代码见一面1.4节。
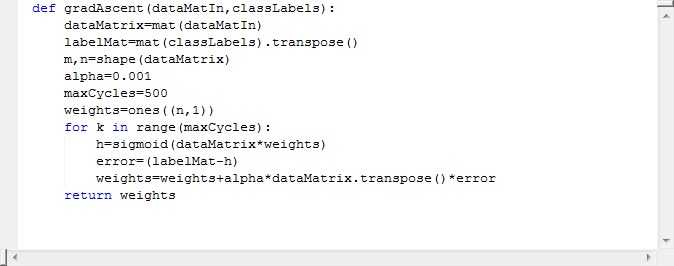
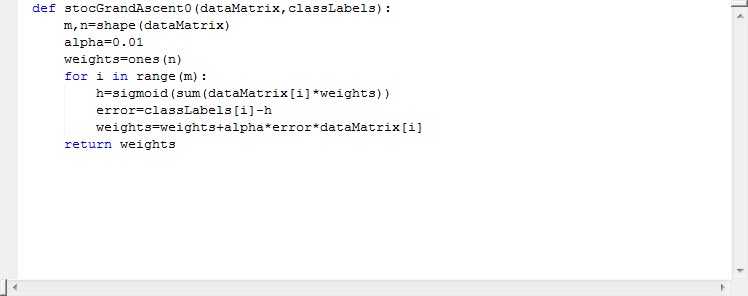
Alpha表示步长,maxcycles表示最大的迭代次数,其中weights=ones((n,1))是初始化一个全部为一的n*1的矩阵。Error就是分类错误的项。大家对于公式:
weights=weights+alpha*dataMatrix.transpose()*error 表示权值是前一个权值+步长*方向(预测值与实际值的差值决定了方向)。
这里没什么好说的,就是把两个特征值分别作为横坐标和纵坐标,然后用一条直线分割开来。
1.4.1梯度上升算法效果图
可以看出分错了四个点,但是这个方法计算量太大了。大家来跟着我改进它!
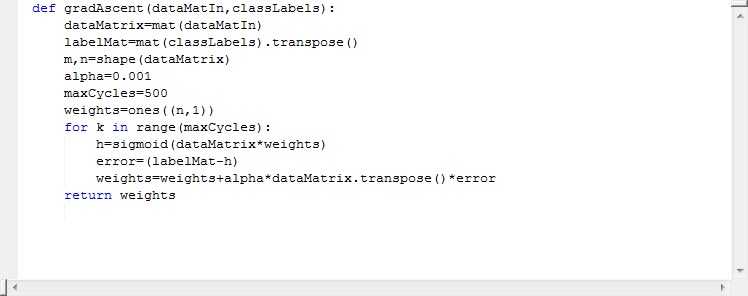
1.4.2随机梯度上升。
实现代码如下:
梯度上升算法在每次更新回归系数的时候都需要遍历整个数据集,这样处理数十亿样本或者成千上万的特征,那还不爆炸么,计算复杂度太高了。一种改进方法是一次仅用一个样本点来更新回归系数,该方法称为梯度上升算法。要根据给出的数据边学习边给结果,所以随机梯度上升算法是一个在线学习算法。
效果图:
等等,小花你在逗我吧。你这个越改越差。刚开始,我们的分类器那么完美,你现在分类的结果是个什么东东啊。哈哈,其实这个游戏本身就是不公平的,梯度上升算法,在整个数据集上迭代了500次才得到的,而第二种才计算了几次。而且判断一个算法优劣的可靠方法是看它是否收敛,也就是随着计算次数的增加参数是否趋于稳定。大家莫急,先等我略施小计。
1.4.2改进的随机梯度上升算法
代码如下:
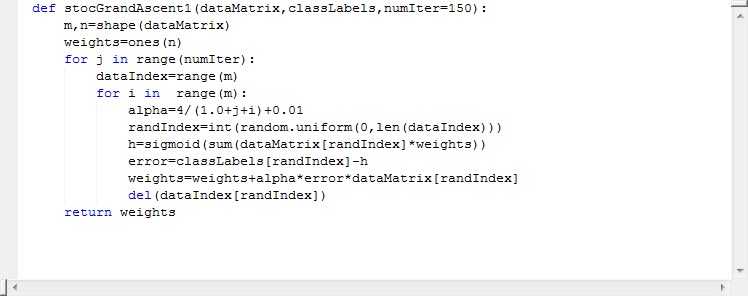
(1) 让步长变化,加上一个参数表示步长永远不会等于0,保持每次加的数据都会对结果又影响。
(2) 有一个随机的过程从数据集中选取数据来更新参数,选到之后就不选了。
(3) 参数设定,这里设定的是150次迭代,等下我设置500次让大家看看实验结果。
150次迭代如下:
500次迭代如下:
感觉好像没什么变化啊。这就是随机上升梯度算法的奥妙啊。迭代150次和500次一样,这样对时间复杂度的减少意义重大啊,有木有。
2.1准备数据:处理数据的缺失值
方法:
1. 删除
最简单的方法是删除,删除属性或者删除样本。如果大部分样本该属性都缺失,这个属性能提供的信息有限,可以选择放弃使用该维属性;如果一个样本大部分属性缺失,可以选择放弃该样本。虽然这种方法简单,但只适用于数据集中缺失较少的情况。
2. 统计填充
对于缺失值的属性,尤其是数值类型的属性,根据所有样本关于这维属性的统计值对其进行填充,如使用平均数、中位数、众数、最大值、最小值等,具体选择哪种统计值需要具体问题具体分析。另外,如果有可用类别信息,还可以进行类内统计,比如身高,男性和女性的统计填充应该是不同的。
3. 统一填充
对于含缺失值的属性,把所有缺失值统一填充为自定义值,如何选择自定义值也需要具体问题具体分析。当然,如果有可用类别信息,也可以为不同类别分别进行统一填充。常用的统一填充值有:“空”、“0”、“正无穷”、“负无穷”等。
4. 预测填充
我们可以通过预测模型利用不存在缺失值的属性来预测缺失值,也就是先用预测模型把数据填充后再做进一步的工作,如统计、学习等。虽然这种方法比较复杂,但是最后得到的结果比较好。
2.2 测试算法
代码:
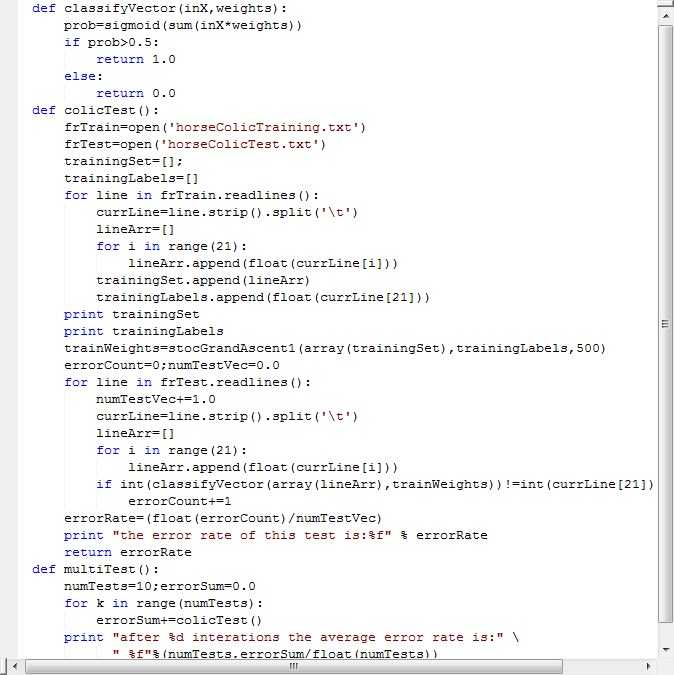
实验结果:
总结:为什么输出的结果不一样呢,因为里面有一个随机的值啊。
毕竟自己也是在学习,如有错误,请大家不吝赐教。
机器学习实战------利用logistics回归预测病马死亡率
标签:
原文地址:http://www.cnblogs.com/xiaohuahua108/p/5936705.html