UVA11538 - Chess Queen（数学组合）

标签：

题目链接：https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2533

题意：在n*m的棋盘上放两个(黑和白)相互攻击的皇后，求有多少种方法？  0<=(n,m)<=10e6;

下图是2*2的方案数12；

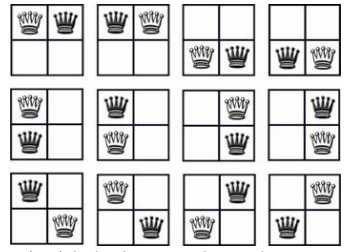
很明显要按行列还有对角三种来考虑，每种的方案数相加即可；

每一行我们要从m个格子中选择2个进行放所以方案数是m*(m-1)，共有n行，所以有 n*m*(m-1) 种；同样可知每一列有n个格子，所以相对应的方案数有m*n*(n-1);

对角有两种我们可以讨论其中一种为，然后乘2即可；

当n<=m时 所有的/向的对角线，从左到右的长度依次为1,2,3,4,...n-1,n,n,...n,n,n-1,n-2,...2,1;(一共有m-n+1个n);

所以对角的情况 = 2*（2*∑(i*(i-1))(i=1 -> i=n-1)+(m-n+1)*n*(n-1)）;

∑(i*(i-1)) = ∑i^{2 -} ∑i = n*(n-1)*(2*n-1)/6 - n*(n-1)/2 = n*(n-1)*(2*n-4)/3; 即所有的对角情况 = 2n(n-1)(3*m-n-1)/3

 ans = n*m*(m-1)  +  m*n*(n-1)  +  2n(n-1)(3*m-n-1)/3;

#include <stdio.h>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <map>
using namespace std;
typedef long long LL;
#define met(a, b) memset(a, b, sizeof(a))
const int N = 200060;
const double eps = 1e-6;
const int INF = 0x3f3f3f3f;
const int mod = 10007;

int main()
{
    LL  n, m, ans;
    while(scanf("%lld %lld", &n, &m), m+n)
    {
        if(n > m) swap(m, n);
        ans = n*m*(m-1) + n*m*(n-1) + 2*n*(n-1)*(3*m-n-1)/3;
        printf("%lld\n", ans);
    }
    return 0;
}

View Code

UVA11538 - Chess Queen（数学组合）

标签：

原文地址：http://www.cnblogs.com/zhengguiping--9876/p/5939365.html