标签:
今天在微信上看到一篇介绍如何判断单向链表是否有环的文章,感觉很有意思,整理一下读后的思路。
一、判断单向链表是否有环
方法1:设置一个Hashset,顺序读取链表中的节点,判断Hashset中是否有该节点的唯一标识(ID)。如果在Hashset中,说明有环;如果不在Hashset中,将节点的ID存入Hashset。
这种方法时间复杂度已经最优,但是因为额外申请了Hashset,所以空间复杂度不算最优。
方法2:设置2个指针,指向头节点。第1个指针每次指向下一个节点;第2个指针指向下一个节点的下一个节点(可以大致理解为,第1个指针每次加1,第2个指针每次加2)。如果第2个指针指向null,说明到达链表结尾,链表中没有环;如果链表中有环,一定会在环上的某个节点处,两个指针同时指向同一个节点。这就是追击相遇的问题。
文章的作者提到了为什么两个指针一定会在环上相遇,做了一个类比,运动员沿跑道跑步,一个快一个慢,二人无限循环,两人一定在某个位置再次相遇,就是所谓的扣圈。但是个人觉得这只是一个类比,不能真正的证明有环链表同样适用。毕竟人跑步是一个连续的问题,而链表的追击问题是一个离散的问题。
我的理解,假设在慢指针进入环的时候,快指针到慢指针的距离为n;那么下一次移动的时候,快指针到慢指针的距离将缩小为(n-1);再下次,为(n-2);即每次移动,距离缩小1,如此往复,两个指针的距离最终将变成0。而且从慢指针进入环开始计算,到二者相遇,一定经过了n次的移动。
二、求环的长度
因为有上面的结论(从慢指针进入环开始计算,到二者相遇,一定经过了n次的移动)。相似的,可以得到如下结论,假设环长为R,从二者在环上第一次相遇,到二者在还上第二次相遇,一定经过了R次移动。
因此,只要记录二者从第一次相遇到第二次相遇一共移动了多少步,就知道环长了。
三、求环的起点的位置
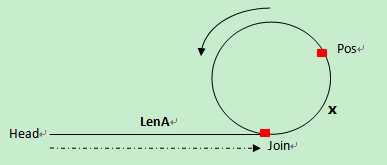
假设起点到环起点的长度为LenA;开始到第一次相遇,移动了t步;环的长度为R;环的起点到二者第一次相遇位置的距离为x,二者相遇的时候快指针已经在环上转了n圈。
则有如下等式成立: 慢指针移动的距离=LenA + x; 即 t = LenA + x;
快指针移动的距离=LenA + n * R + x; 即 2t = LenA + n * R + x;
所以 2*(LenA+x) = LenA + n*R + x;
即 LenA = n * R - x;
上面的等式可以这样理解,如果慢指针从链表起点开始移动,快指针从环起点开始移动,当慢指针从起点走到环起点的时候,快指针一直在环上移动,而且还差x步就移动了n圈。进而可以得到结论,如果慢指针从链表起点开始移动,快指针从二者第一次相遇点开始移动,当慢指针到达环起点的时候,快指针也正好达到环起点,即二者指向相同的节点。
可以参考图片(从另一篇博客黏贴,博客地址:求有环单链表中的环长、环起点、链表长):
四、求链表长
有了二中的环长R和三中的LenA,二者相加就是链表长。
五、无聊的补充
后来坐车的时候想到这样一个东西,可能没什么用途,先记录下来。当慢指针到达环起点时,假设这时快指针在PosB处,PosB距离环起点的距离也是x。
标签:
原文地址:http://www.cnblogs.com/huanyou/p/5944296.html