标签:
考虑到数据结构短板严重,从计算几何换换口味= =
简介
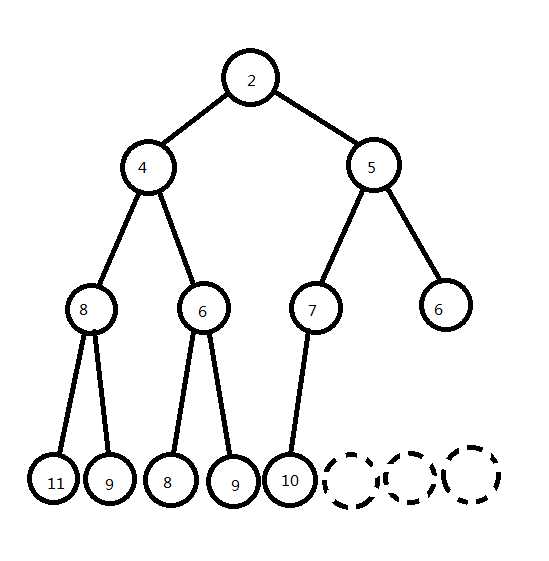
堆总保持每个节点小于(大于)父亲节点。这样的堆被称作大根堆(小根堆)。
顾名思义,大根堆的数根是堆内的最大元素。
堆的意义在于能快速O(1)找到最大/最小值,并能持续维护。
复杂度
push() = O(logn);
pop() = O(logn);
BinaryHeap() = O(nlogn);
实现
数组下标从1开始的情况下,有
Parent(i) = i >> 1
LChild(i) = i << 1
RChild(i) = i << 1 + 1
实现 up() 和 down() 方法达到上浮,下沉
题目分析
题目要求
在c个元素中选出n(奇数)个元素,在a权值和小于F的情况下,求b权值中位数的最大值。
Handle
中位数的性质:两边元素个数相等。
解题思路
先按b权值升序排序,建两个大根堆,从n/2到c-n/2枚举中位数,维护前半段和后半段的a权值的n/2个最小值。
维护方法:若 b[i] < b[heap.top()] 则 pop() 并 push(i)。
代码比较丑 凑合看吧
//POJ 2010
//题目概述:数学题,状态转移
//二叉堆的应用,卡排序,BBS()过不了
//这个AC异常艰辛 总共提交11次 充分体现了锲而不舍的精神
//AC 2016-10-15
#include <cstdio>
#include <algorithm>
using namespace std;
#define MAXC 100000 + 10
#define MAXN 20000 + 10
struct node{
int val, cost;
friend bool operator < (const node &n1, const node &n2){
return n1.val < n2.val;
}
friend bool operator > (const node &n1, const node &n2){
return n1.val > n2.val;
}
}p[MAXC];
struct BHeap{
node heap[MAXC];
int n;
BHeap(): n(0){}
void clear(){n = 0;}
void down(int i){
for (int j = i * 2; j <= n; j *= 2){
j += (j < n) && (heap[j].cost < heap[j + 1].cost);
if (heap[j].cost > heap[i].cost){
swap(heap[i], heap[j]);
i = j;
}
else break;
}
}
void up(int i){
for (int j = i / 2; j >= 1; j /= 2){
if (heap[j].cost < heap[i].cost){
swap(heap[i], heap[j]);
i = j;
}
else break;
}
}
node &pop(){
swap(heap[1], heap[n--]);
down(1);
return heap[n + 1];
}
node &top(){
return heap[1];
}
void push(node &a){
heap[++n] = a;
up(n);
}
}heap;
int before[MAXC], after[MAXC];
int main(){
int n, c, f, minval = 0x7f7f7f7f;
freopen("fin.c", "r", stdin);
while (scanf("%d%d%d", &n, &c, &f) + 1){
for (int i = 1; i <= c; i++){
scanf("%d%d", &p[i].val, &p[i].cost);
}
sort(p + 1, p + 1 + c);
int size = n / 2;
heap.clear();
before[size + 1] = 0;
for (int i = 1; i <= size; i++){
heap.push(p[i]);
before[size + 1] += p[i].cost;
}
for (int i = size + 1; i < c - size; i++){
if (heap.top().cost > p[i].cost){
before[i + 1] = before[i] - heap.pop().cost + p[i].cost;
heap.push(p[i]);
}
else before[i + 1] = before[i];
}
heap.clear();
after[c - size] = 0;
for (int i = c; i > c - size; i--){
heap.push(p[i]);
after[c - size] += p[i].cost;
}
for (int i = c - size; i > size + 1; i--){
if (heap.top().cost > p[i].cost){
after[i - 1] = after[i] - heap.pop().cost + p[i].cost;
heap.push(p[i]);
}
else after[i - 1] = after[i];
}
for (int i = c - size; i >= size + 1; i--){
if (after[i] + before[i] + p[i].cost <= f){
printf("%d\n", p[i].val);
goto END;
}
}
puts("-1"); END:;
}
}
POJ 2010 - Moo University - Financial Aid 初探数据结构 二叉堆
标签:
原文地址:http://www.cnblogs.com/xlnx/p/5965705.html