标签:
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 6098 | Accepted: 2671 |
Description
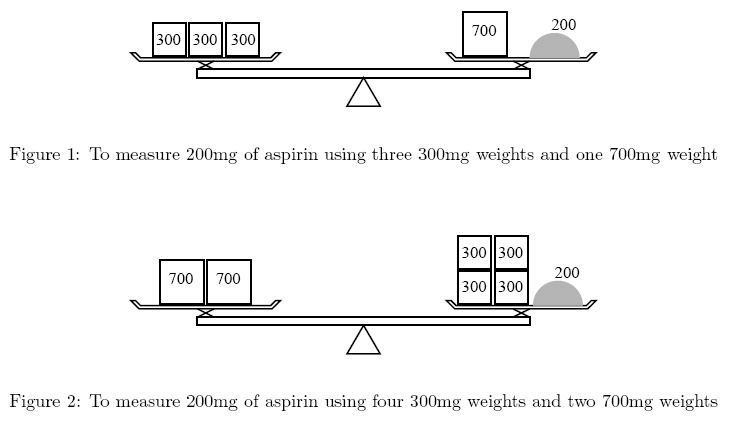
Input
Output
Sample Input
700 300 200 500 200 300 500 200 500 275 110 330 275 110 385 648 375 4002 3 1 10000 0 0 0
Sample Output
1 3 1 1 1 0 0 3 1 1 49 74 3333 1
Source
分析
假设 a 砝码我们用了 x 个,b 砝码我们用了 y 个。那么天平平衡时,就应该满足
ax+by==c。x,y 为正时表示放在和 c 物品的另一边,为负时表示放在 c 物品的同一边。于
是题意就变成了求|x|+|y|的最小值了。x 和 y 是不定式 ax+by==c 的解。刚刚上面已经提到
了关于 x,y 的所以解的同式,即
x=x0+b/d*t
y=y0-a/d*t
穷举所有解,取|x|+|y|最小的?显然是行不通的,仔细分析:
|x|+|y|==|x0+b/d*t|+|y0-a/d*t|,我们规定 a>b(如果 a<b,我们便交换 a b),从这个式子
中,我们可以轻易的发现:|x0+b/d*t|是单调递增的,|y0-a/d*t|是单调递减的,而由于我们
规定了 a>b,那么减的斜率边要大于增的斜率,于是整个函数减少的要比增加的快,但是
由于绝对值的符号的作用,最终函数还是递增的。也就是说,函数是凹的,先减小,再增
大。那么什么时候最小呢?很显然是 y0-a/d*t==0 的时候,于是我们的最小值|x|+|y|也一定
是在 t=y0*d/a 附近了,只要在附近枚举几个值就能找到最优解了。
1 #include <cstdio> 2 #include <cmath> 3 #include <cstring> 4 #include <cstdlib> 5 #include <queue> 6 #include <stack> 7 #include <vector> 8 #include <iostream> 9 #include "algorithm" 10 using namespace std; 11 typedef long long LL; 12 int a,b,c,d; 13 int x,y; 14 int exgcd(int a,int b,int &x,int &y){ 15 if (b==0) 16 {x=1; 17 y=0; 18 return a; 19 } 20 int d=exgcd(b,a%b,x,y); 21 int t=x; 22 x=y; 23 y=t-(a/b)*y; 24 return d; 25 } 26 int main(){ 27 freopen ("balance.in","r",stdin); 28 freopen ("balance.out","w",stdout); 29 int i,j; 30 bool flag; 31 while (1) 32 {scanf("%d%d%d",&a,&b,&c); 33 if (!(a || b || c)) 34 break; 35 flag=false; 36 if (a<b) 37 {swap(a,b); 38 flag=true; 39 } 40 d=exgcd(a,b,x,y); 41 x*=(c/d),y*=(c/d); 42 int t,ax,ay,zx,zy; 43 t=y/(a/d); 44 ax=abs(x+b/d*t); 45 ay=abs(y-a/d*t); 46 for (i=1;i<=10;i++) 47 {zx=abs(x+b/d*(t+i)); 48 zy=abs(y-a/d*(t+i)); 49 if ((zx+zy<ax+ay) || (zx+zy==ax+ay && zx*a+zy*b<ax*a+ay*b)) 50 {ax=zx; 51 ay=zy; 52 } 53 zx=abs(x+b/d*(t-i)); 54 zy=abs(y-a/d*(t-i)); 55 if ((zx+zy<ax+ay) || (zx+zy==ax+ay && zx*a+zy*b<ax*a+ay*b)) 56 {ax=zx; 57 ay=zy; 58 } 59 } 60 if (flag) 61 swap(ax,ay); 62 printf("%d %d\n",ax,ay); 63 } 64 return 0; 65 }
标签:
原文地址:http://www.cnblogs.com/keximeiruguo/p/5971726.html