标签:
题目:
Given an array S of n integers, are there elements a, b, c, and d in S such that a + b + c + d = target?
Find all unique quadruplets in the array which gives the sum of target.
Note: The solution set must not contain duplicate quadruplets.
For example, given array S = [1, 0, -1, 0, -2, 2], and target = 0.
A solution set is:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
官方难度:
Medium
翻译:
给定一个长度为n的整形数组,是否存在4个元素a,b,c,d,使a+b+c+d=给定值target?
找出所有的可能解。
注意:解集中不能包含重复解。
例子:
给定数组 S = [1, 0, -1, 0, -2, 2],目标值target=0,解集为:
[-1, 0, 0, 1],[-2, -1, 1, 2],[-2, 0, 0, 2]
思路:
1. 与之前做过的2Sum,3Sum是一类的题目,3Sum Colsest勉强也可以算这一类的题目,可以称之为KSum类型的题目,除了2Sum题目使用了取巧的方法(实际上,就效率而言,可能并不是那么高效),将数组转成集合,利用了List.contains()方法,其余的做法基本都一致:使用多重循环将KSun问题转化为(K-1)Sum问题,那么自然而然的就想到,可以使用递归的方法,对这一类问题做出一个通解。
2. 既然是递归问题,自然需要先明确递归的终点,显然,递归的终点是2Sum问题。
3. 由于解法的时间复杂度相对较高,时间复杂度为O(nlogn)的排序算法是值得的。
4. 分析KSum问题的入参,需要:数组array,目标值target,问题类型kSum。
5. 分析KSum问题的返回值,是Set<int[]>类型的。
6. 针对KSum(K>2)的情况,开启循环,循环的结束条件是i<array.length-(kSum-1),因为考虑到要对剩余的数组做(K-1)Sum问题的递归,剩余的数组元素的个数要有保证。
7. tempTarget=target-array[i],作为(K-1)Sum问题入参中的目标值target。
8. (K-1)Sum问题入参中的数组是Arrays.copyOfRange(array,i+1,array.length)。
9. 将(K-1)Sum问题的结果集和当前数字array[i]组装起来,加入KSum问题的结果集。
10. 针对递归终点2Sum,因为数组有序,可以使用Arrays.binarySearch()方法,注意方法入参的数组用剩余数组,不要使用原数组。
解题中可能遇到的困难:
1. 因为数组需要排序,但这又是一个递归的问题,实际上只要一次排序就够了,如果不做控制,会增加很多无谓排序
的时间消耗。有两种解决方案:控制仅仅在第一次进入方法时排序;或者保证入参的数组已经有序。我采用的是前面一种做法。
2. 因为是有序数组,所以无论是2Sum还是KSum(k>2),只要有array[i+1]>tempTarget且array[i+1]>0,就可以直接return了,因为后面的数字会越来越大,不可能存在匹配。
3. 可以维护一个lastNumber,记录上一次循环中出现的数字,若与当前的数字相等直接continue。
4. 3中的做法,最初的时候我以为只是“可以这么做”,但是结果实际上是“必须这么做”,因为对于一个Set<int[]>结构的返回值,两个一模一样的数组并不会由于Set集合的特性而被去重。看下面一个例子:
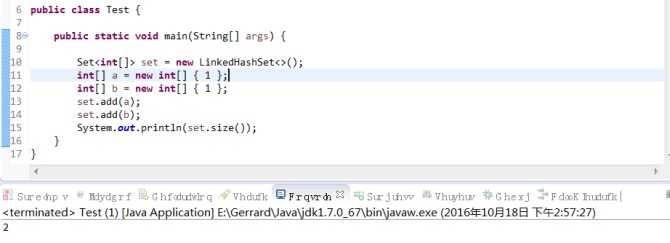
5. 针对以上出现的问题,一开始的想法是对原数组做一次去重的操作,但实际上是错误的。很简单的理由,试想:数组[4,-2,-2,0],target=0,如果对数组去重,那解集就不存在了。但是维护lastNumber却不会出现这种情况,因为这只是减少了重复劳动,不会对解集产生影响。
6. 记得做入参检查的处理。
解题代码:

1 private static Set<int[]> method(int[] array, int target, int kSum) { 2 // 入参保护 3 if (array == null || array.length < kSum) { 4 return null; 5 } 6 // 第一次进来做一次排序,之后自然有序,无需排序 7 if (kSum == 4) { 8 Arrays.sort(array); 9 } 10 // 结果集 11 Set<int[]> result = new LinkedHashSet<>(); 12 // 递归终点是2Sum问题 13 if (kSum == 2) { 14 if (target < array[0]) { 15 // 因为数组有序,target如果小于数组第一项,返回空集合 16 return result; 17 } else { 18 int lastNumber = Integer.MAX_VALUE; 19 for (int i = 0; i < array.length - 1; i++) { 20 if (array[i] == lastNumber) { 21 continue; 22 } 23 int tempTarget = target - array[i]; 24 // 秉承始终向后找的思想,下一项小于tempTarget,且下一项大于0,直接退出 25 // 而且tempTarget会越来越小,array[i+1]越来越大,再往后更加不可能了,直接返回 26 if (tempTarget < array[i + 1] && array[i + 1] > 0) { 27 return result; 28 } 29 int[] remainArray = Arrays.copyOfRange(array, i + 1, array.length); 30 int index = Arrays.binarySearch(remainArray, tempTarget); 31 if (index >= 0) { 32 int[] newArray = new int[2]; 33 newArray[0] = array[i]; 34 newArray[1] = remainArray[index]; 35 result.add(newArray); 36 37 } 38 lastNumber = array[i]; 39 } 40 } 41 } else { 42 // 大于2Sum问题,使用递归 43 // 记录上一个值,这是必须的,因为Set集合对于2个一模一样的数组无能为力 44 int lastNumber = Integer.MAX_VALUE; 45 for (int i = 0; i < array.length - (kSum - 1); i++) { 46 if (array[i] == lastNumber) { 47 continue; 48 } 49 int tempTarget = target - array[i]; 50 if (array[i + 1] > tempTarget && array[i + 1] > 0) { 51 return result; 52 } 53 // 开启递归 54 Set<int[]> tempResult = method(Arrays.copyOfRange(array, i + 1, array.length), tempTarget, kSum - 1); 55 for (int[] a : tempResult) { 56 int[] newArray = new int[a.length + 1]; 57 newArray[0] = array[i]; 58 for (int j = 0; j < a.length; j++) { 59 newArray[j + 1] = a[j]; 60 } 61 result.add(newArray); 62 } 63 // 下次循环前,变更lastNumber 64 lastNumber = array[i]; 65 } 66 } 67 return result; 68 }
测试代码地址:
LeetCode题目地址:
https://leetcode.com/problems/4sum/
PS:如有不正确或提高效率的方法,欢迎留言,谢谢!
标签:
原文地址:http://www.cnblogs.com/jing-an-feng-shao/p/5973421.html