标签:
数据作为信息的载体,要分析数据中包含的主要信息,即要分析数据的主要特征(即数据的数字特征), 对于数据的数字特征, 包含数据的集中位置、分散程度和数据分布,常用统计项目如下:
集中趋势
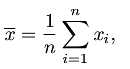
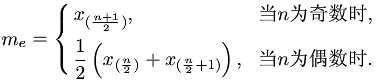
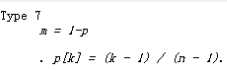
离散趋势
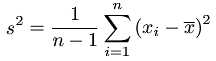
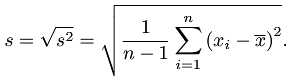
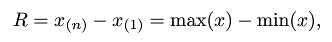
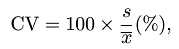
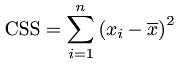
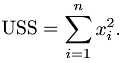
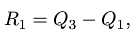
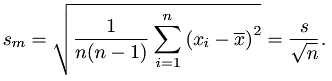
分布情况统计


示例函数
setwd("E:\\R")
myDescriptStat <- function(x){
n <- length(x) #样本数据个数
m <- mean(x) #均值
me <- median(x) #中位数
mo <- names(table(x))[which.max(table(x))] #众数
sd <- sd(x) #标准差
v <- var(x) #方差
r <- max(x) - min(x) #极差
cv <- 100 * sd/m #变异系数
css <- sum(x - m)^2 #样本校正平方和
uss <- sum(x^2) #样本未校正平方和
R1 <- quantile(x,0.75) - quantile(x,0.25) #四分位差
sm <- sd/sqrt(n) #标准误
g1 <- n/((n-1)*(n-2)*sd^3)*sum((x-m)^3)/sd^3 #偏度系数
g2 <- ((n*(n+1))/((n-1)*(n-2)*(n-3))*sum((x-m)^4)/sd^4 -(3*(n-1)^2)/((n-2)*(n-3))) #峰度系数
data.frame(N=n,Mean=m,Median=me,Mode=mo,
Std_dev=sd,Variance=v,Range=r,
CV=cv,CSS=css,USS=uss,
R1=R1,SM=sm,Skewness=g1,Kurtosis=g2,
row.names=1)
}
示例结果如下:
> setwd("E:\\R")
> source("myDescriptStat.R")
> w<-c(75.0,64.0,47.4,66.9,62.2,62.2,58.7,63.5,66.6,64.0,57.0,69.0,56.9,50.0,72.0) #学生体重
> myDescriptStat(w)
N Mean Median Mode Std_dev Variance Range CV CSS USS R1 SM
1 15 62.36 63.5 62.2 7.514823 56.47257 27.6 12.05071 2.019484e-28 59122.16 8.9 1.940319
Skewness Kurtosis
1 -0.001013136 0.09653947
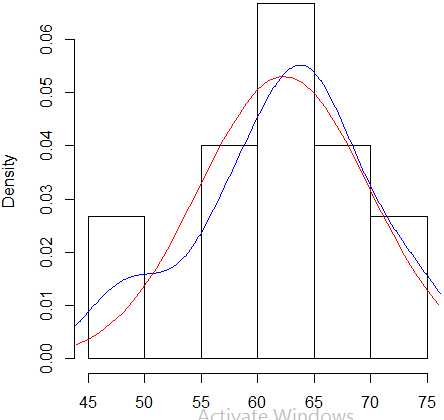
绘学生的体重的直方图和核密度估计图,并与正态分布的概率密度函数作对照图,代码及示例:
hist(w,freq=FALSE) lines(density(w),col="blue") x<-44:76 lines(x,dnorm(x,mean(w),sd(w)),col="red")
标签:
原文地址:http://www.cnblogs.com/tgzhu/p/5961176.html