标签:
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 19782 | Accepted: 6393 |
Description

Input
Output
Sample Input
7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0
Sample Output
8 4000
Hint
/*/ 大二这学期开学真是忙爆了。作为一个班干部,天哪。。 好久没有刷题了,想起以前听了岛娘的一节课,单调栈,好像有点似懂非懂,于是抽时间看了一下,总算是搞通了。。。 将读入的数据一个个压栈,奖数据与栈顶进行比较大小,如果这个数比栈顶小,就计算以站顶为高的最大矩形的大小,弹出栈顶。如果这个数比栈顶大,直接就压进栈。这样一系列操作之后,就会发现栈里面剩下一个递增数列,用一个pair来保存此时栈高度和前面达到这个高度的个数,然后按照前面的思想去计算每一个高度最大矩形面积是多大。
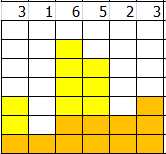
AC代码: /*/
#include "stdio.h"
#include "string.h"
#include "stack"
#include "algorithm"
using namespace std;
typedef long long LL;
typedef pair<LL,LL> PII;
const LL MX = 1e5 + 5;
int main() {
LL n,h;
while(~scanf("%lld",&n)) {
if(n==0)break;
stack<PII> Q;
while(!Q.empty()) {
Q.pop();
}
LL ans=0;
for(LL i=0; i<n; i++) {
scanf("%lld",&h);
LL Now_Big_W=0;
while(!Q.empty() && Q.top().first >= h ) {
LL H = Q.top().first;
LL W = Q.top().second;
Q.pop();
Now_Big_W+=W;
ans=max(ans,H*Now_Big_W);
}
Q.push(PII(h,Now_Big_W+1));
}
LL The_number_W=0;
while(!Q.empty()){
The_number_W+=Q.top().second;
ans=max(ans,Q.top().first*The_number_W);
Q.pop();
}
printf("%lld\n",ans);
}
return 0;
}
poj 2559 Largest Rectangle in a Histogram - 单调栈
标签:
原文地址:http://www.cnblogs.com/HDMaxfun/p/5983230.html