AVL学习笔记

时间：2016-10-22 17:50:09 阅读：244 评论：0 收藏：0 [点我收藏+]

标签：struct 大于最大值分享 break number alt 状态 val

AVL，平衡二叉查找树。删除，插入，查找的复杂度都是O(logn)。它是一棵二叉树。对于每个节点来说，它的左孩子的键值都小于它，右孩子的键值都大于它。对于任意一个节点，它的左右孩子的高度差不大于1。树的高度的定义为：空节点的高度为0，非空节点的高度为左右孩子高度的最大值加1。

在插入删除过程中，会出现不平衡的时候。这时，会通过以下方式进行旋转保持树的平衡。下图中每一列最后一行是旋转后的结果，上面两行是对应的初始化状态。

技术分享

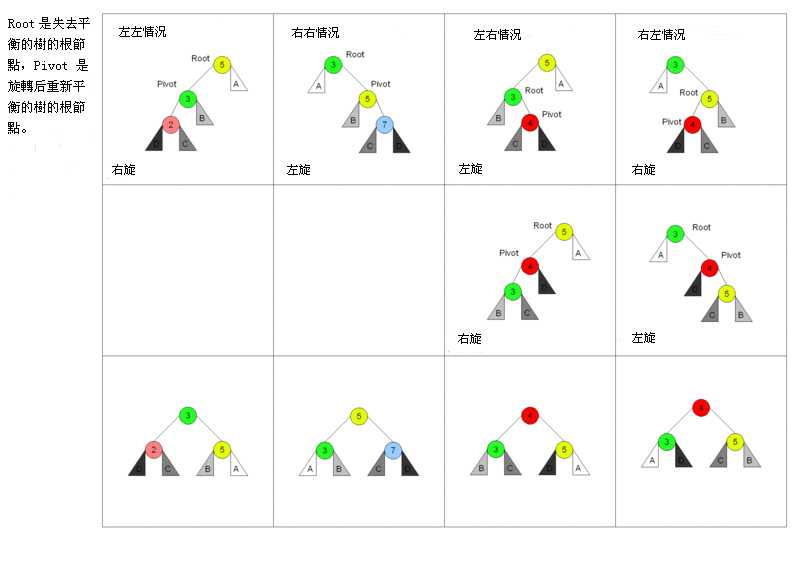
1 插入。在以某个节点为根的子树中插入一个节点后，有可能使得该节点的左右子树的高度差大于1（其实此时的高度差是2），那么视情况进行LL，RR，LR，RL四种旋转中的一种可维持树的平衡。

2 删除。删除的键值小于当前节点键值时，在左子树中删除；大于当前节点键值时在右子树中进行删除；否则就是删除当前节点。删除当前节点时，找到后继节点，然后将后继结点替换当前节点，然后递归地删除这个后继结点即可。

template<class _ValyeType,class _FuncType>
class CAVLTree
{
protected:
    struct AVLTreeNode
    {
        _ValyeType m_iValue;
        AVLTreeNode* m_pLeftSon;
        AVLTreeNode* m_pRightSon;
        int m_nHeight;
        int m_nValueNumber;
    };
    AVLTreeNode* m_pRoot;
    _FuncType* m_pCompareFunc;

    AVLTreeNode* _NewNode()
    {
        AVLTreeNode* pNode=new AVLTreeNode;
        pNode->m_pLeftSon=nullptr;
        pNode->m_pRightSon=nullptr;
        pNode->m_nHeight=1;
        pNode->m_nValueNumber=0;
        return pNode;
    }
    AVLTreeNode* _NewNode(const _ValyeType& iValue)
    {
        AVLTreeNode* pNode=new AVLTreeNode;
        pNode->m_pLeftSon=nullptr;
        pNode->m_pRightSon=nullptr;
        pNode->m_nHeight=1;
        pNode->m_iValue=iValue;
        pNode->m_nValueNumber=1;
        return pNode;
    }

    int _Height(AVLTreeNode* pNode)
    {
        if(pNode) return pNode->m_nHeight;
        return 0;
    }

    void _PushUp(AVLTreeNode* pNode)
    {
        if(!pNode) return;
        const int nLeftSonHeight=_Height(pNode->m_pLeftSon);
        const int nRightSonHeight=_Height(pNode->m_pRightSon);
        if(nLeftSonHeight<nRightSonHeight) pNode->m_nHeight=1+nRightSonHeight;
        else pNode->m_nHeight=1+nLeftSonHeight;
    }

    /**
       pNode的左孩子将成为根,返回新的树根
    **/
    AVLTreeNode* _LLRotate(AVLTreeNode* pNode)
    {
        if(!pNode) return pNode;
        AVLTreeNode* pLeftSon=pNode->m_pLeftSon;
        pNode->m_pLeftSon=pLeftSon->m_pRightSon;
        pLeftSon->m_pRightSon=pNode;
        _PushUp(pNode);
        _PushUp(pLeftSon);
        return pLeftSon;
    }


    /**
       pNode的右孩子将成为根,返回新的树根
    **/
    AVLTreeNode* _RRRotate(AVLTreeNode* pNode)
    {
        if(!pNode) return pNode;
        AVLTreeNode* pRightSon=pNode->m_pRightSon;
        pNode->m_pRightSon=pRightSon->m_pLeftSon;
        pRightSon->m_pLeftSon=pNode;
        _PushUp(pNode);
        _PushUp(pRightSon);
        return pRightSon;
    }
    /**
        pNode的左孩子的右孩子将成为根,返回新的树根
    **/
    AVLTreeNode* _LRRotate(AVLTreeNode* pNode)
    {
        if(!pNode) return pNode;
        pNode->m_pLeftSon=_RRRotate(pNode->m_pLeftSon);
        return _LLRotate(pNode);
    }

    /**
        pNode的右孩子的左孩子将成为根,返回新的树根
    **/
    AVLTreeNode* _RLRotate(AVLTreeNode* pNode)
    {
        if(!pNode) return pNode;
        pNode->m_pRightSon=_LLRotate(pNode->m_pRightSon);
        return _RRRotate(pNode);
    }

    AVLTreeNode* _Rotate(AVLTreeNode* pNode)
    {
        if(!pNode) return pNode;
        if(2==_Height(pNode->m_pLeftSon)-_Height(pNode->m_pRightSon))
        {
            if(_Height(pNode->m_pLeftSon->m_pLeftSon)>=_Height(pNode->m_pLeftSon->m_pRightSon))
            {
                pNode=_LLRotate(pNode);
            }
            else pNode=_LRRotate(pNode);
        }
        else if(2==_Height(pNode->m_pRightSon)-_Height(pNode->m_pLeftSon))
        {
            if(_Height(pNode->m_pRightSon->m_pLeftSon)>=_Height(pNode->m_pRightSon->m_pRightSon))
            {
                pNode=_RLRotate(pNode);
            }
            else pNode=_RRRotate(pNode);
        }
        return pNode;
    }

    AVLTreeNode* _Insert(AVLTreeNode* pRoot,const _ValyeType& iInsertValue)
    {
        if(nullptr==pRoot)
        {
            pRoot=_NewNode(iInsertValue); return pRoot;
        }
        else if(m_pCompareFunc(iInsertValue,pRoot->m_iValue))
        {
            pRoot->m_pLeftSon=_Insert(pRoot->m_pLeftSon,iInsertValue);
            if(2==_Height(pRoot->m_pLeftSon)-_Height(pRoot->m_pRightSon))
            {
                if(m_pCompareFunc(iInsertValue,pRoot->m_pLeftSon->m_iValue))
                {
                    pRoot=_LLRotate(pRoot);
                }
                else
                {
                    pRoot=_LRRotate(pRoot);
                }
            }
        }
        else if(m_pCompareFunc(pRoot->m_iValue,iInsertValue))
        {
            pRoot->m_pRightSon=_Insert(pRoot->m_pRightSon,iInsertValue);
            if(2==_Height(pRoot->m_pRightSon)-_Height(pRoot->m_pLeftSon))
            {
                if(m_pCompareFunc(iInsertValue,pRoot->m_pRightSon->m_iValue))
                {
                    pRoot=_RLRotate(pRoot);
                }
                else
                {
                    pRoot=_RRRotate(pRoot);
                }
            }
        }
        else
        {
            ++pRoot->m_nValueNumber;
        }

        _PushUp(pRoot);
        return pRoot;
    }

    AVLTreeNode* _Delete(AVLTreeNode* pRoot,const _ValyeType& iDeleteValue)
    {
        if(nullptr==pRoot) return nullptr;
        if(m_pCompareFunc(iDeleteValue,pRoot->m_iValue))
        {
            pRoot->m_pLeftSon=_Delete(pRoot->m_pLeftSon,iDeleteValue);
        }
        else if(m_pCompareFunc(pRoot->m_iValue,iDeleteValue))
        {
            pRoot->m_pRightSon=_Delete(pRoot->m_pRightSon,iDeleteValue);
        }
        else
        {
            if(0==--pRoot->m_nValueNumber)
            {
                if(nullptr==pRoot->m_pLeftSon)
                {
                    AVLTreeNode* pTmp=pRoot;
                    pRoot=pRoot->m_pRightSon;
                    delete pTmp;
                }
                else if(nullptr==pRoot->m_pRightSon)
                {
                    AVLTreeNode* pTmp=pRoot;
                    pRoot=pRoot->m_pLeftSon;
                    delete pTmp;
                }
                else
                {
                    AVLTreeNode* pTmp=pRoot->m_pRightSon;
                    while(pTmp->m_pLeftSon) pTmp=pTmp->m_pLeftSon;
                    pRoot->m_iValue=pTmp->m_iValue;
                    pRoot->m_pRightSon=_Delete(pRoot->m_pRightSon,pRoot->m_iValue);
                }
            }
            else
            {
                return pRoot;
            }
        }
        _PushUp(pRoot);
        if(pRoot&&pRoot->m_pLeftSon) pRoot->m_pLeftSon=_Rotate(pRoot->m_pLeftSon);
        if(pRoot&&pRoot->m_pRightSon) pRoot->m_pRightSon=_Rotate(pRoot->m_pRightSon);
        if(pRoot) pRoot=_Rotate(pRoot);
        return pRoot;
    }


public:
    CAVLTree(_FuncType* pCompareFunc):m_pRoot(nullptr),m_pCompareFunc(pCompareFunc) {}

    void Insert(const _ValyeType& iInsertValue)
    {
        m_pRoot=_Insert(m_pRoot,iInsertValue);
    }

    void Delete(const _ValyeType& iDeleteValue)
    {
        m_pRoot=_Delete(m_pRoot,iDeleteValue);
    }

    int Find(const _ValyeType& iSearchValue)
    {
        AVLTreeNode* pCurrent=m_pRoot;
        while(1)
        {
            if(!pCurrent) break;
            if(m_pCompareFunc(iSearchValue,pCurrent->m_iValue))
            {
                pCurrent=pCurrent->m_pLeftSon;
            }
            else if(m_pCompareFunc(pCurrent->m_iValue,iSearchValue))
            {
                pCurrent=pCurrent->m_pRightSon;
            }
            else return pCurrent->m_nValueNumber;
        }
        return 0;
    }

};

AVL学习笔记

标签：struct 大于最大值分享 break number alt 状态 val

原文地址：http://www.cnblogs.com/jianglangcaijin/p/5987767.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行