noip模拟赛 好元素 哈希表的第一题

标签：ash   rom   otto   有趣   sam   计算   转换   线性   快速定位   

这是一道关于

题2好元素

2s

【问题描述】

小A一直认为，如果在一个由N个整数组成的数列{An}中，存在以下情况：

Am+An+Ap = Ai (1 <= m, n, p < i <= N , m,n,p可以相同)，那么Ai就是一个好元素。

现在小A有一个数列，请你计算数列中好元素的数目

【输入格式】

第一行只有一个正整数N，意义如上。

第二行包含N个整数，表示数列{An}。

【输出格式】

输出一个整数，表示这个数列中好元素的个数。

【输入样例】

【输出样例】

【数据范围】

 对于10%的数据1<=N<=10

 对于40%的数据1<=N<=500 -10^5<=Ai<=10^5

 对于70%的数据1<=N<=5000 -10^6<=Ai<=10^6

 对于100%的数据1<=N<=5000 -10^9<=Ai<=10^9

分析：

写这道题会发现数据非常大，而我们如果用n²的方法就会出现很有趣的现象，比如。炸时间。所以我们得用哈希表来解决这个问题。

接下来讲解一下哈希表是什么，及一些神奇的东西：

哈希表，又名散列表，将线性表(或者一群大数据)运用某种散列函数，将数据转化成一种关键字。关键字组成另一种可以用于快速查找的表。快速定位，快速查找是否存在该元素。。很多数据可能有相同的关键字，所以可以将关键字相同的数据连成一个新的线性表。

主要就是写散列函数，而散列函数有很多种写法。没有固定的套路。有些可以讲数据%一个大质数，将整个线性表叠在一个新的线性（但是有链表）的表里。可以用领结表来表现。这有点绕其实就是下图的样子。A[]代表将数据转换成的关键字。后面连起来的东西就是关键字旗下的大数据。

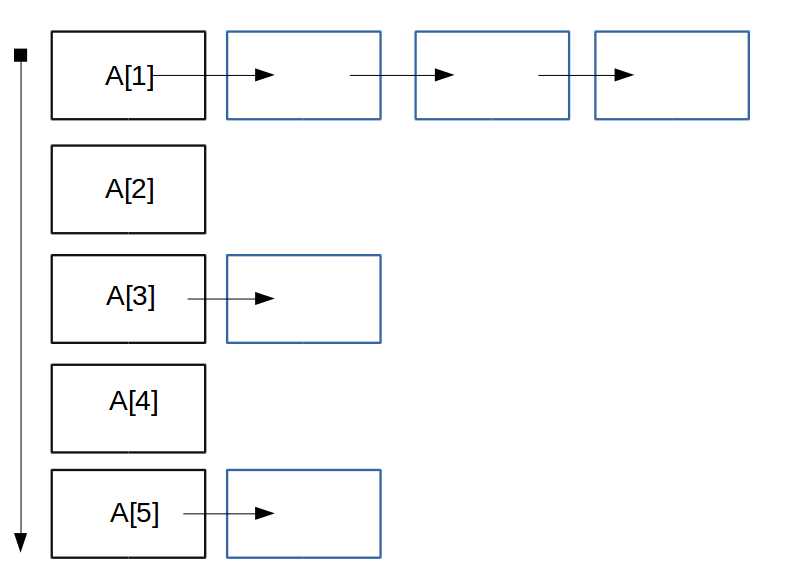
当然有些也会用位运算，将后面几位相同的数组成一个线性序列。这道题其实就用这个方法。

。讲一下这道题的大致做法:

从前往后枚举，每次枚举1，最后的重点,2，前面的一个点，而我们哈希表里放的就是两个数之和，而我们在枚举的时候。可以及时更新哈希表。（在枚举完一个新点，就将这个点与前面的每个点的值的和加入哈希表）。其实就是枚举。但是这里优化时间优化的吓人。所以可以过//hhhhh。

放出代码：

#include<cstdio>
#include<algorithm>
using namespace std;
#define M 4194303
int line[5001];
int n,cnt;
int hashline[M+1];
int vale[12600001];
int next[12600001];
void address(int w)
{
    vale[++cnt]=w;
    next[cnt]=hashline[w & M];
    hashline[w & M]=cnt;
    return ;
}
bool pure(int w)
{
    for(int i=hashline[w & M]; i ; i=next[i])
    {
        if(vale[i]==w)return true;
    }
    return false;
}
int ref()
{
    int ans=0;
    for(int i=1;i<=n;++i)
    {
        for(int j=1;j<i;++j)
        {
            if(pure(line[i]-line[j]))
            {
                ++ans;
                break;
            }
        }
        for(int j=1;j<=i;++j){
            address(line[i]+line[j]);
        }
    }
    return ans;
}
int main()
{
    freopen("good.in","r",stdin);
    freopen("good.out","w",stdout);
    scanf("%d",&n);
    for(int i=1;i<=n;++i)scanf("%d",&line[i]);
    int ans=ref();
    printf("%d",ans);
    fclose(stdin);
    fclose(stdout);
    return 0;
}

就是这样的东西。这个我认为比较好理解。还有就是。这个4194303数选的特别玄学。如果选小了。还过不了了？！！！！

noip模拟赛 好元素 哈希表的第一题

标签：ash   rom   otto   有趣   sam   计算   转换   线性   快速定位   

原文地址：http://www.cnblogs.com/uncle-lu/p/5994279.html