标签:数据 简单 string long div 优化 接下来 max 方案
最短路问题是图论中的经典问题,求解单源最短路问题可以采用dijkstra算法,时间复杂度O(n^2),使用堆优化后可以达到O(nlogn)。在稀疏图中也可用spfa算法,并不比dijkstra算法表现的差。当然如果有负权值回路,dijkstra就只能GG了!求解全图中任意两点的最短路径还可以用floyd算法,时间复杂度O(n^3),虽然复杂度较高,但在需要的时候该算法也可表现的很好。求两点间的最短路径则可以通过深搜或广搜实现,时间复杂度O(m)。
当然最短路问题可以有很多变形,比如下面几道题。
Problem 1:[luogu P2384] 最短路
给定n个点的带权有向图,求从1到n的路径中边权之积最小的简单路径。
输入格式:
第一行读入两个整数n,m,表示共n个点m条边。 接下来m行,每行三个正整数x,y,z,表示点x到点y有一条边权为z的边。
输出格式:
输出仅包括一行,记为所求路径的边权之积,由于答案可能很大,因此你输出它模9987的余数即可。
3 3 1 2 3 2 3 3 1 3 10
9
对于20%的数据,n<=10。
对于100%的数据,n<=1000,m<=1000000。边权不超过10000。
本题是最短路径的变形,我们可以用类比法,用更新边权加和的策略来更新边权乘积,由于本题数据较水,裸spfa即可通过。
1 #include <cstdio> 2 #include <iostream> 3 #include <algorithm> 4 using namespace std; 5 6 int n,m,l,pre[1000005],last[1005],other[1000005]; 7 int que[1000005]; 8 long long len[1000005],d[1000005]; 9 bool vis[1000005]; 10 11 void add(int u,int v,int r) { 12 pre[++l]=last[u]; 13 last[u]=l; 14 other[l]=v; 15 len[l]=r; 16 } 17 18 int main() { 19 scanf("%d%d",&n,&m); 20 for (int i=1; i<=m; i++) { 21 int x,y,z; 22 scanf("%d%d%d",&x,&y,&z); 23 add(x,y,z); 24 add(y,x,z); 25 } 26 for (int i=1; i<=n; i++) d[i]=2147483647; 27 d[1]=1; 28 que[1]=1; 29 int h=0, t=1; 30 while (h<t) { 31 int cur=que[++h]; 32 vis[cur]=0; 33 for (int p=last[cur]; p ;p=pre[p]) { 34 int q=other[p]; 35 if (d[q]>d[cur]*len[p]) { 36 d[q]=d[cur]*len[p]; 37 if (!vis[q]) { 38 vis[q]=1; 39 que[++t]=q; 40 } 41 } 42 } 43 } 44 printf("%lld",d[n]); 45 return 0; 46 }
Problems 2:[福建省历届夏令营] 房间最短路问题
在一个长宽均为10,入口出口分别为(0,5)、(10,5)的房间里,有几堵墙,每堵墙上有两个缺口,求入口到出口的最短路经。
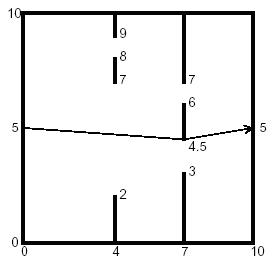
输入格式:
第一排为n(n<=20),墙的数目。
接下来n排,每排5个实数x,a1,b1,a2,b2。
x表示墙的横坐标(所有墙都是竖直的),a1-b1和a2-b2之间为空缺。
a1、b1、a2、b2保持递增,x1-xn也是递增的。
输出格式:
输出最短距离,保留2位小数。
2 4 2 7 8 9 7 3 4.5 6 7
10.06
本题属于比较简单的最短路建模问题。不难发现沿着墙角与墙角之间的直线走是最优的。
把图中所有点都找出(墙角的点和起点终点),两两建边(当两点连线不被墙隔开时)。
跑一边最短路即可求解。
1 #include <cstdio> 2 #include <iostream> 3 #include <algorithm> 4 #include <cmath> 5 using namespace std; 6 7 int n,tot,l,pre[100050],last[100050],other[100050],que[100050]; 8 bool vis[100050]; 9 double x[1050],y[1050]; 10 double xx[25],a[25],b[25],c[25],d[25],len[100050],dis[100050]; 11 12 double minn(double x,double y) { 13 if (x>y) return y; 14 return x; 15 } 16 17 double maxx(double x,double y) { 18 if (x<y) return y; 19 return x; 20 } 21 22 void add(int u,int v,double r) { 23 pre[++l]=last[u]; 24 last[u]=l; 25 other[l]=v; 26 len[l]=r; 27 } 28 29 int main() { 30 scanf("%d",&n); 31 for (int i=1; i<=n; i++) { 32 scanf("%lf %lf %lf %lf %lf",&xx[i],&a[i],&b[i],&c[i],&d[i]); 33 tot++; 34 x[tot]=xx[i]; 35 y[tot]=a[i]; 36 tot++; 37 x[tot]=xx[i]; 38 y[tot]=b[i]; 39 tot++; 40 x[tot]=xx[i]; 41 y[tot]=c[i]; 42 tot++; 43 x[tot]=xx[i]; 44 y[tot]=d[i]; 45 } 46 int s=++tot; x[s]=0; y[s]=5; 47 int t=++tot; x[t]=10; y[t]=5; 48 for (int i=1; i<=tot; i++) { 49 for (int j=1; j<=tot; j++) { 50 if (i==j) continue; 51 if (x[i]==x[j]) { 52 for (int k=1; k<=n; k++) { 53 if (xx[k]==x[i]) { 54 if ((y[i]==a[k] && y[j]==b[k]) || (y[i]==b[k] && y[j]==a[k]) || (y[i]==c[k] && y[j]==d[k]) || (y[i]==d[k] && y[j]==c[k])) { 55 double length=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])); 56 add(i,j,length); 57 break; 58 } 59 } 60 } 61 continue; 62 } 63 bool f=0; 64 for (int k=1; k<=n; k++) { 65 if (xx[k]<=minn(x[i],x[j])) continue; 66 if (xx[k]>=maxx(x[i],x[j])) break; 67 double p=(xx[k]-x[j])*(y[i]-y[j])/(x[i]-x[j])+y[j]; 68 if ((p>=0 && p<=a[k]) || (p>=b[k] && p<=c[k]) || (p>=d[k])) { 69 f=1; 70 break; 71 } 72 } 73 if (!f) { 74 double length=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])); 75 add(i,j,length); 76 } 77 } 78 } 79 for (int i=1; i<=tot; i++) dis[i]=2147483637; 80 dis[s]=0; 81 que[1]=s; 82 int he=0,ta=1; 83 while (he<ta) { 84 int cur=que[++he]; 85 vis[cur]=0; 86 for (int p=last[cur]; p ;p=pre[p]) { 87 int q=other[p]; 88 if (dis[q]>dis[cur]+len[p]) { 89 dis[q]=dis[cur]+len[p]; 90 if (!vis[q]) { 91 vis[q]=1; 92 que[++ta]=q; 93 } 94 } 95 } 96 } 97 printf("%.2lf",dis[t]); 98 return 0; 99 }
Problem 3:[luogu P1144] 最短路计数
给出一个N个顶点M条边的无向无权图,顶点编号为1~N。问从顶点1开始,到其他每个点的最短路有几条。
输入格式:
输入第一行包含2个正整数N,M,为图的顶点数与边数。
接下来M行,每行两个正整数x, y,表示有一条顶点x连向顶点y的边,请注意可能有自环与重边。
输出格式:
输出包括N行,每行一个非负整数,第i行输出从顶点1到顶点i有多少条不同的最短路,由于答案有可能会很大,你只需要输出mod 100003后的结果即可。如果无法到达顶点i则输出0。
5 7 1 2 1 3 2 4 3 4 2 3 4 5 4 5
1 1 1 2 4
1到5的最短路有4条,分别为2条1-2-4-5和2条1-3-4-5(由于4-5的边有2条)。
对于20%的数据,N ≤ 100;
对于60%的数据,N ≤ 1000;
对于100%的数据,N ≤ 100000,M ≤ 200000。
本题属于求最短路方案数的问题,在能转移的状态下记下转移数,累加即可得解。本题数据较大,建议用dijkstra+堆优化。
1 #include <cstdio> 2 #include <iostream> 3 #include <algorithm> 4 #include<iostream> 5 #include<vector> 6 #include<cstring> 7 #include<queue> 8 using namespace std; 9 const int maxn=100005; 10 vector<int> G[maxn]; 11 int d[maxn],ans[maxn]; 12 int main() { 13 int n,m; 14 scanf("%d%d",&n,&m); 15 for(int i=0,x,y;i<m;i++) { 16 scanf("%d%d",&x,&y); 17 G[x].push_back(y); 18 G[y].push_back(x); 19 } 20 queue<int> q; 21 memset(d,-1,sizeof(d)); 22 d[1]=0; 23 ans[1]=1; 24 q.push(1); 25 while(!q.empty()) { 26 int u=q.front(); 27 q.pop(); 28 for(int i=0;i<G[u].size();i++) { 29 int v=G[u].at(i); 30 if(d[v]==-1) { 31 d[v]=d[u]+1; 32 ans[v]=ans[u]; 33 q.push(v); 34 } else { 35 if(d[v]==d[u]+1) { 36 ans[v]+=ans[u]; 37 ans[v]%=100003; 38 } 39 } 40 } 41 } 42 for(int i=1;i<=n;i++) printf("%d\n",ans[i]); 43 return 0; 44 }
标签:数据 简单 string long div 优化 接下来 max 方案
原文地址:http://www.cnblogs.com/zoewilly/p/5994740.html