标签:ges add while pad 默认 思路 void ted --
20161026模拟赛解题报告
By shenben
T1
按照题目说的模拟即可
但这题有一个神坑:当25个字母都已经一一对应完毕后,剩下的两个字母默认对应。
T2
所有的逆序对之间都会连边,求最大独立点集。
表面上是个图论题,其实是个LIS
O(nlogn)求最长上升子序列的长度即可AC
T3
第一次手贱,用链表存边,这是一个稠密图啊!!应该用邻接矩阵啊。
明明可以用floyed跑,非要dfs乱搞。结果10分。玩砸了吧。
最后只改到了40分。
网上的题解(没看懂):
首先这是一个神奇的图,叫做竞赛图。大概定义就是每两点之间都有且仅有一条有向边,看这题就非常好理解了。
竞赛图有一个很好的性质:只要存在环,环中点的个数就一定大于等于3个。
证明:
根据定义,一元环和二元环显然不存在。
于是考虑多元环:
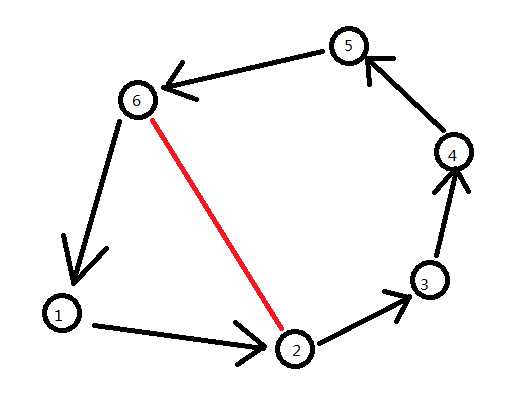
我们知道在2与6之间会有一条边,如果这条边从2指向6,那么就形成了1-2-6三元环,否则我们会发现原本的六元环变成了6-2-3-4-5组成的五元环,环变小了。
当这个环缩小到四元环时,显然2与4之间的连线无论是哪个方向都会形成三元环。
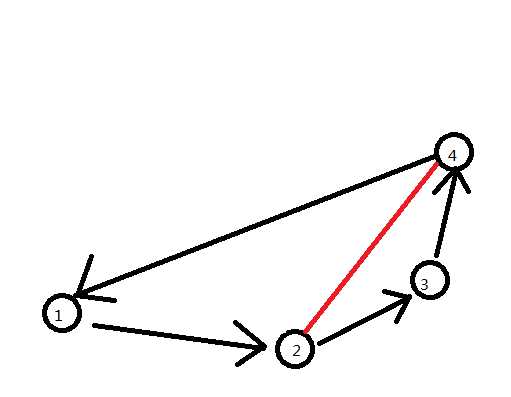
证毕。
然后我们的思路就清晰了:找到一个环,然后按照上述方式即可输出结果。
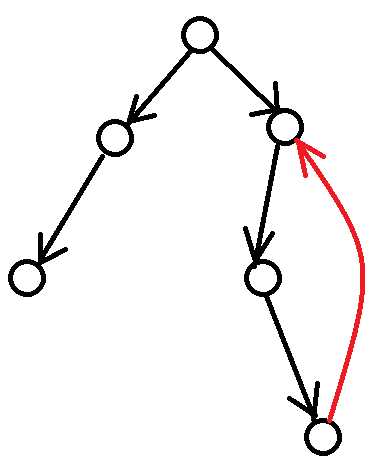
找环的方式则可以采用dfs:
选定一个mark[i]=−1(没有被遍历过)的点,以它为根向下dfs,将沿途上的点mark值设为1,若再次访问则就找到环了。
T1代码(100分)
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; const int N=1e4+10; char s[N],a[N],b[N],f[N]; bool vis[N]; int Q[N>>2],q[N>>2]; int lena,lenb,lens; void Go_special(){ int p=0; for(int i=‘a‘;i<=‘z‘;i++) if(!vis[i]){p=i;break;} vis[p]=1; for(int i=0;i<lena;i++) q[i+1]=a[i]; sort(q+1,q+lena+1); int cnt=unique(q+1,q+lena+1)-(q+1); for(int i=0;i<26;i++) Q[i+1]=i+‘a‘; for(int i=1;i<=26;i++) if(Q[i]!=q[i]){f[p]=Q[i];return ;} } int main(){ freopen("enc.in","r",stdin); freopen("enc.ans","w",stdout); scanf("%s%s%s",a,b,s); lena=strlen(a); lenb=strlen(b); lens=strlen(s); if(lena!=lenb){puts("ERROR");return 0;} for(int i=0;i<lenb;i++){ if(vis[b[i]]&&f[b[i]]!=a[i]){puts("ERROR");return 0;} else vis[b[i]]=1,f[b[i]]=a[i]; } /*for(int i=‘a‘;i<=‘z‘;i++){ for(int j=i+1;j<=‘z‘;j++){ if(f[i]==f[j]) {puts("ERROR");return 0;} } }*/ int tot=0; for(int i=‘a‘;i<=‘z‘;i++) if(f[i]) tot++; if(tot==25) Go_special(); for(int i=0;i<lens;i++) if(!vis[s[i]]){puts("ERROR");return 0;} for(int i=0;i<lens;i++) putchar(f[s[i]]); return 0; }
T2代码(100分)
#include<cstdio> #include<iostream> #include<algorithm> using namespace std; inline const int read(){ register int x=0,f=1; register char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=(x<<3)+(x<<1)+ch-‘0‘;ch=getchar();} return x*f; } const int N=1e5+10; int n,len,a[N],b[N]; int main(){ freopen("sort.in","r",stdin); freopen("sort.ans","w",stdout); n=read(); for(int i=1;i<=n;i++) a[i]=read(); b[len=1]=a[1]; for(int i=2,pos;i<=n;i++){ if(a[i]>b[len]){ b[++len]=a[i]; } else{ pos=lower_bound(b+1,b+len+1,a[i])-b; b[pos]=a[i]; } } printf("%d",len); return 0; } /*int n,ans,a[N]; vector<int>p[N]; void deal(int x){ int cnt=unique(p[x].begin(),p[x].end())-p[x].begin(); ans+=n-1-cnt; } int main(){ freopen("sh.txt","r",stdin); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",a+i); for(int i=1;i<=n;i++){ for(int j=n;j>i;j--){ if(a[j]<a[j-1]){ swap(a[i],a[j]); p[a[i]].push_back(a[j]); p[a[j]].push_back(a[i]); } } } for(int i=1;i<=n;i++) deal(a[i]); printf("%d",ans); return 0; }*/
T3代码(40分)
#include<cstdio> using namespace std; const int N=1e5+10; struct node{ int v,next; }e[N<<1]; int n,tot,qi,head[N]; char mp[N]; int ans[4],sans[4]={9,9,9,9}; bool flag,sflag; void add(int x,int y){ e[++tot].v=y; e[tot].next=head[x]; head[x]=tot; } void record(){ sflag=1; for(int i=1;i<=3;i++) if(ans[i]>sans[i]) return ; for(int i=1;i<=3;i++) sans[i]=ans[i]; } void dfs(int x,int de){ if(de==3){ for(int i=head[x];i;i=e[i].next) if(e[i].v==qi){ans[de]=x;record();break;} return ; } for(int i=head[x];i;i=e[i].next){ ans[de]=x; dfs(e[i].v,de+1); } } int main(){ freopen("game.in","r",stdin); freopen("game.ans","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%s",mp+1); for(int j=1;j<=n;j++){ if(mp[j]==‘1‘) add(i,j); } } for(int i=1;i<=n;i++) dfs(qi=i,1); if(sflag) for(int i=1;i<=3;i++) printf("%d ",sans[i]); else puts("-1"); return 0; }
标签:ges add while pad 默认 思路 void ted --
原文地址:http://www.cnblogs.com/shenben/p/6000712.html