标签:ted represent 时间 line sts ict pos app other
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 5252 | Accepted: 2165 |

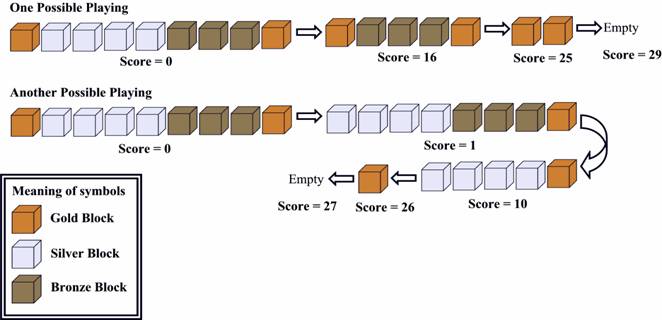
2 9 1 2 2 2 2 3 3 3 1 1 1
Case 1: 29 Case 2: 1
lrj出的题好劲啊......写的TA爷的做法
一个比较厉害的状态$f[l][r][k]$表示当$a[l]==a[r]$时,将$l~r$这个整段玩到还剩连续的$k$个$a[l]/a[r]$色的块时得到的最大的值。
但是单靠这个是不足以转移的,
另一个状态$g[l][r]$表示,不管以什么方法,删光$l~r$这段的得到的最大的值。
然后进行区间DP,显然要枚举区间,枚举断点,转移就是;
$$f[l][r][k]=max(f[l][r][k],f[l][r][k-1]+g[k‘-1][r-1]);$$
这个转移就是把区间$l~r$中花式删掉$k‘~r-1$这段,剩下的组成$k$个的最大方案。
$$g[l][r]=max(g[l][r],f[l][r][k]+k*k,g[l][k‘]+g[k‘+1][r]);$$
这个转移比较显然..
然后这样转移之后,显然$f[l][r][0]=g[l][r]$.
答案就是$f[1][N][0]/g[1][N]$,时间复杂度是$<=O(N^4)$的,而且在正常的数据下表现非常优秀。
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; inline int read() { int x=0,f=1; char ch=getchar(); while (ch<‘0‘ || ch>‘9‘) {if (ch==‘-‘) f=-1; ch=getchar();} while (ch>=‘0‘ && ch<=‘9‘) {x=x*10+ch-‘0‘; ch=getchar();} return x*f; } int T,N,a[210],f[210][210][210],g[210][210],t,cnt[210][210]; int main() { T=read(); while (T--) { N=read(); for (int i=1; i<=N; i++) a[i]=read(); memset(cnt,0,sizeof(cnt)); for (int i=1; i<=N; i++) for (int j=i+1; j<=N; j++) if (a[i]==a[j]) for (int k=i; k<=j; k++) if (a[k]==a[i]) cnt[i][j]++; memset(f,128,sizeof(f)); memset(g,0,sizeof(g)); for (int i=1; i<=N; i++) g[i][i]=f[i][i][0]=1,f[i][i][1]=0; for (int len=1; len<=N; len++) for (int l=1; l+len-1<=N; l++) { int r=l+len-1; for (int i=1; i<=cnt[l][r]; i++) { for (int j=l; j<r; j++) f[l][r][i]=max(f[l][r][i],f[l][j][i-1]+g[j+1][r-1]); g[l][r]=max(g[l][r],f[l][r][i]+i*i); } for (int i=l; i<r; i++) g[l][r]=max(g[l][r],g[l][i]+g[i+1][r]); f[l][r][0]=g[l][r]; } printf("Case %d: %d\n",++t,f[1][N][0]); } return 0; }
标签:ted represent 时间 line sts ict pos app other
原文地址:http://www.cnblogs.com/DaD3zZ-Beyonder/p/6005384.html