标签：均值 图片 使用 one 目标 ret 方差 oat 偏差
改系列只为记录我学习 udacity 中深度学习课程！！
1. 整个课程分为四个部分，如上图所示。
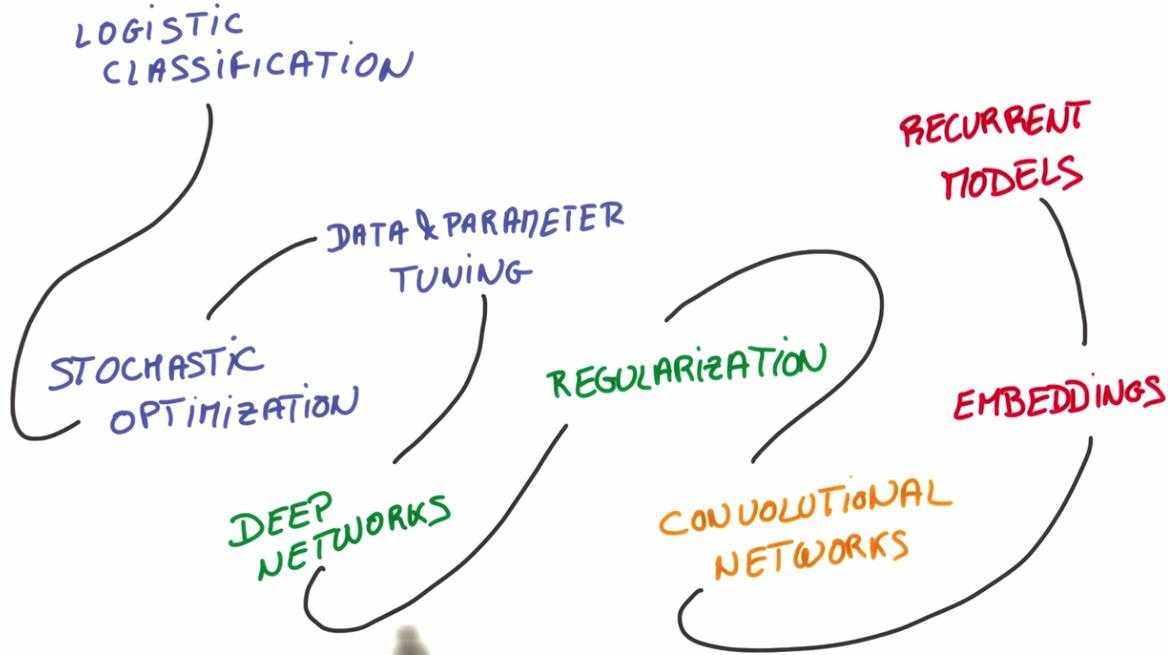
第一部分将研究逻辑分类器，随机优化以及实际数据训练。
第二部分我们将学习一个深度网络，和使用正则化技术去训练一个更大的模型
第三部分我们将深入研究图像和卷积模型
第四部分我们将学习文本和序列，我们将训练嵌入和递归模型
2. 课程将注重分类问题的研究
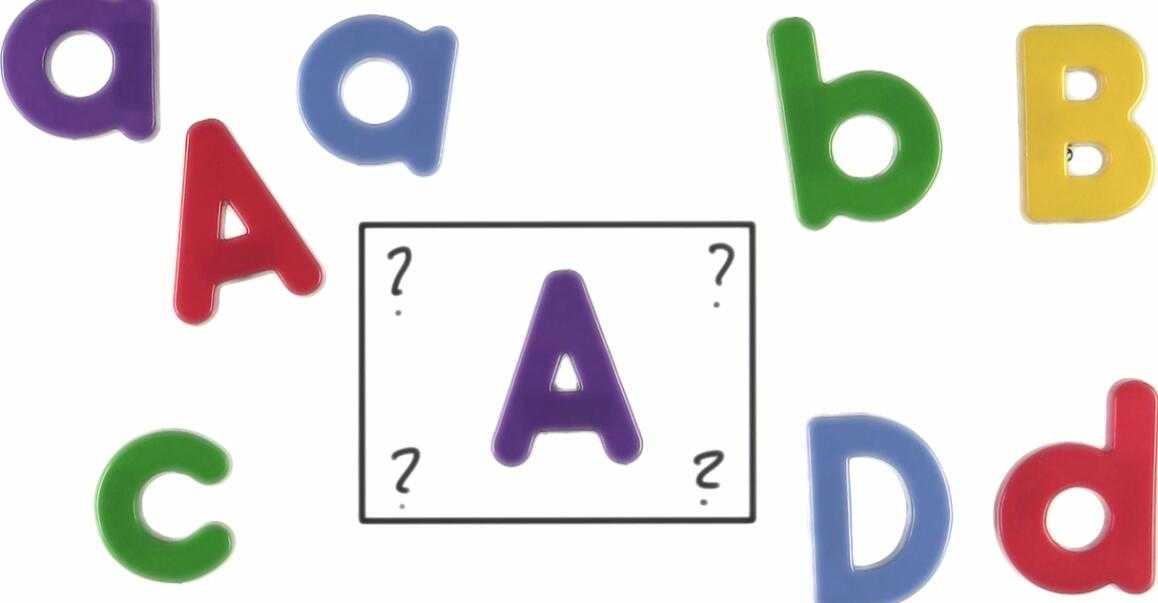
分类问题：典型的情况是你有很多样本，我们称为训练数据集，我们已经把他们归类了。
现在有一个全新的样本，你的目标是要指出这个样本属于哪一类？
3. 机器学习中不只是分类问题，但分类是整个机器学习的基石！
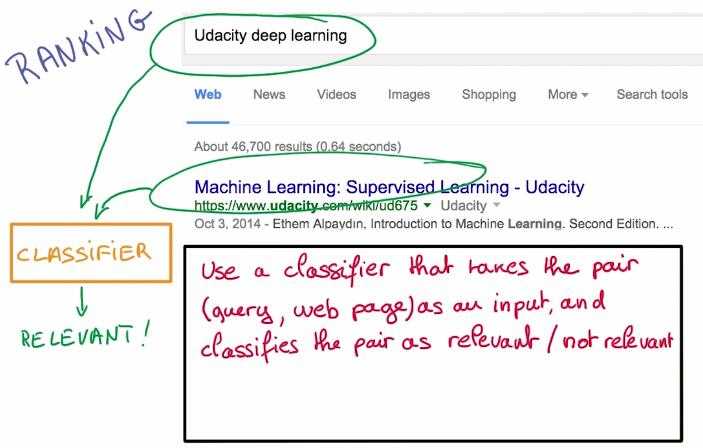
第二张图中，如果我们想做到行人检测，我们可以设计一个分类器将图中的小块分为行人/非行人两类，当分类器输入行人时，就要告诉我们行人的位置。
第三张图中，如果我们想做到网页搜索，我们可以使分类器接收成对的搜索请求，网页的输出则是相关/不相关两类。
4. 逻辑分类器是一种线性分类器
它接收输入X，比如图片的像素，对输入执行一个线性函数来生成预测，称为评分函数，该函数就是一个巨大的矩阵乘法。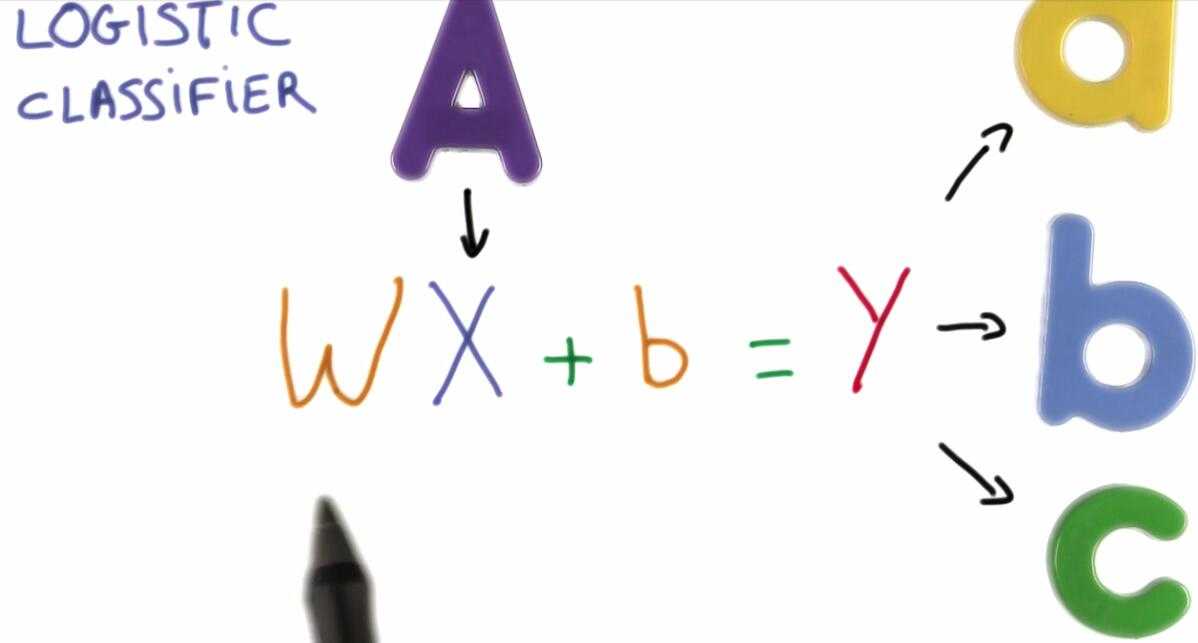
其中 W 是权重weights， b 是偏置项bias.
机器学习的目的就是为了找到一 W&b 使得我们的预测结果表现的非常好。
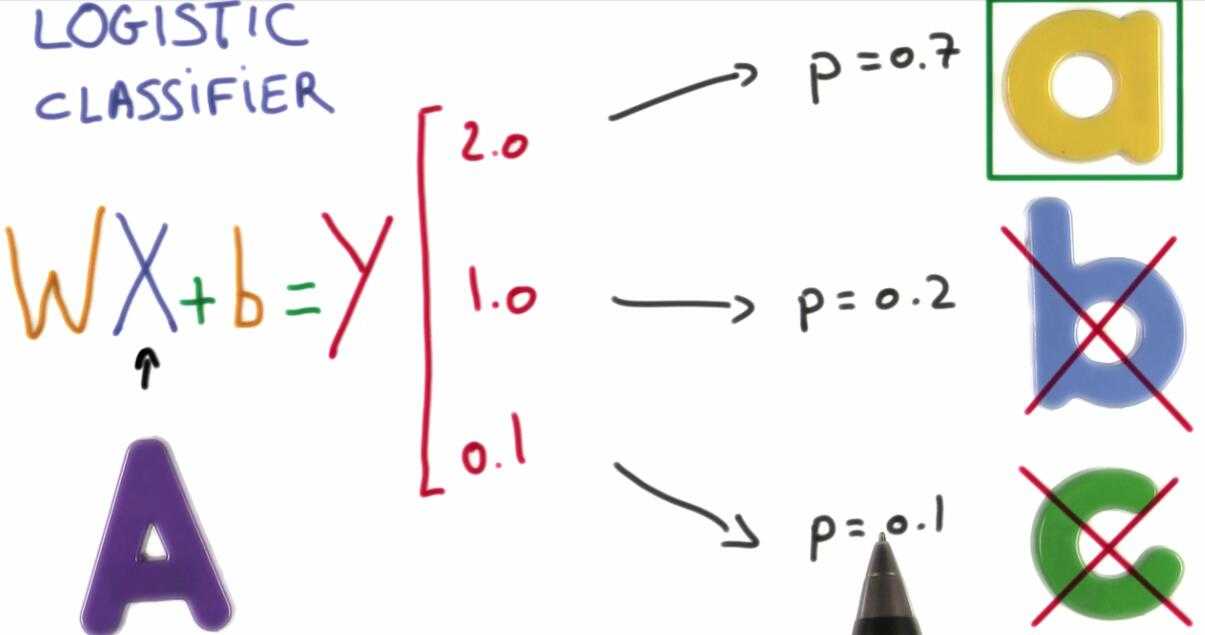
我们如果用上面的结果来执行分类呢？
我们将这些结果转化成概率，这将使得正确的分类概率接近于1，不正确的接近于0.
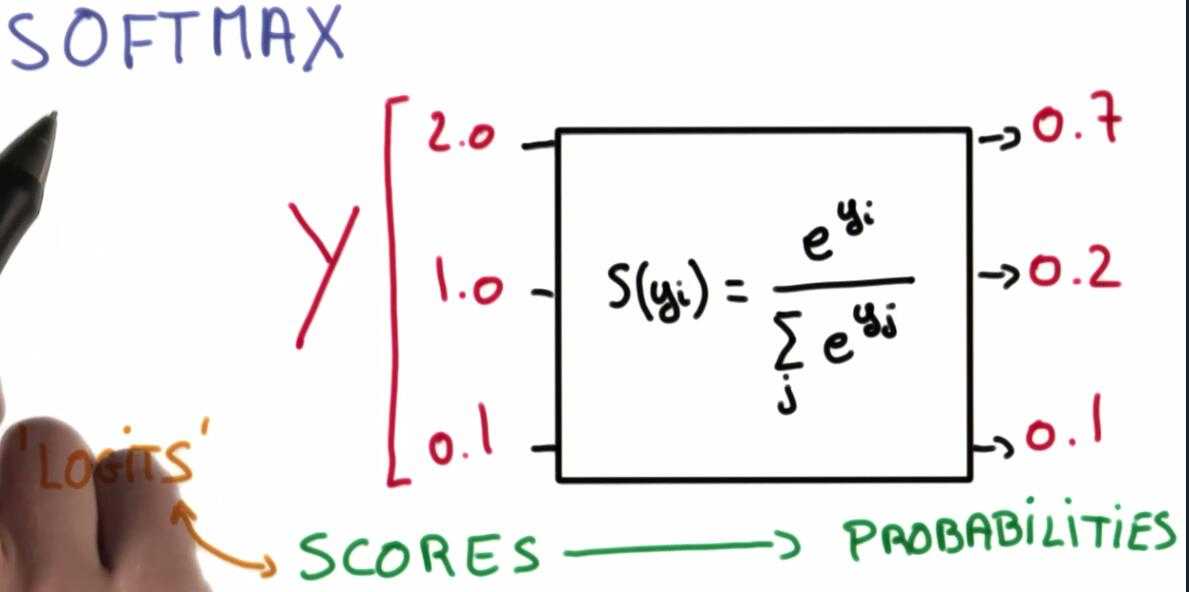
我们将结果转化为概率的方法是使用一个 Softmax 函数
我们将这些结果转化成概率，这将使得正确的分类概率接近于1，不正确的接近于0.
下面是在python中实现 softmax 函数的代码，值得注意的是当线性函数输出数量级较大时 softmax 函数 概率区别度越高，反之乐接近于平均分布。
#coding=utf-8 """Softmax.""" # 假设线性函数输出为三个类别值，设计softmax函数给输出打分，获得分类概率 scores = [3.0, 1.0, 0.2] import numpy as np def softmax(x): """Compute softmax values for each sets of scores in x.""" return np.exp(x) / np.sum(np.exp(x), axis=0) print(softmax(scores)) # Plot softmax curves import matplotlib.pyplot as plt x = np.arange(-2.0, 6.0, 0.1) scores = np.vstack([x, np.ones_like(x), 0.2 * np.ones_like(x)]) plt.plot(x, softmax(scores).T, linewidth=2) plt.show()
5. One-Hot编码
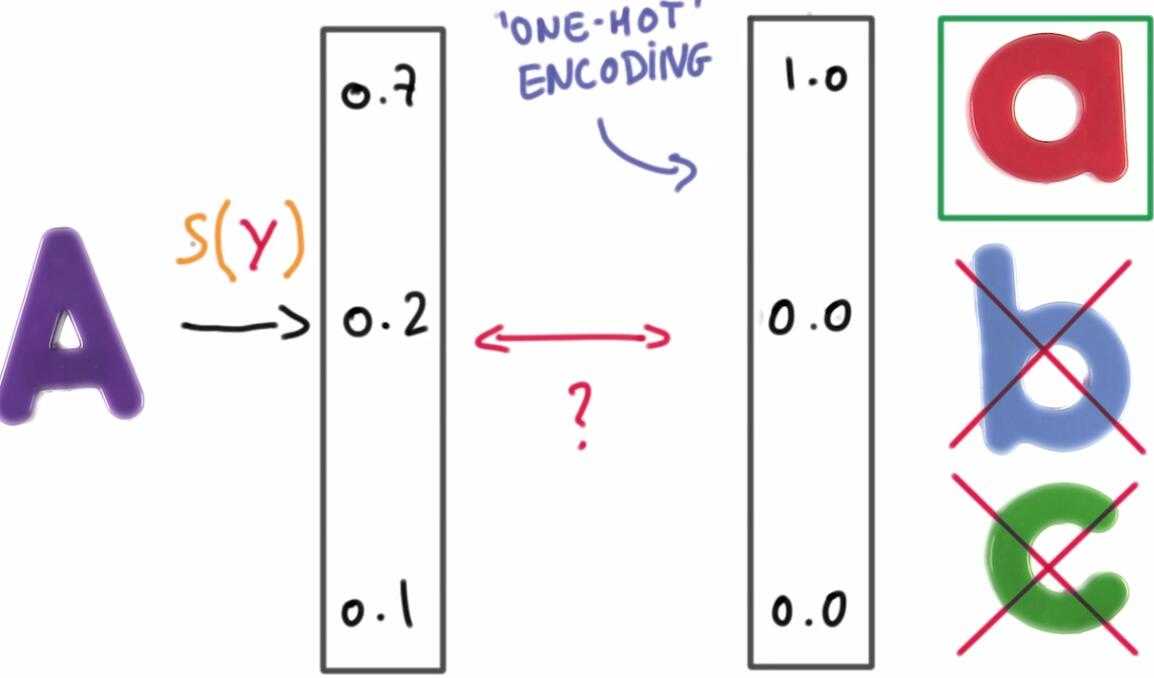目的是使得正确的类别得分为1，不正确的为0
6. cross-entropy loss
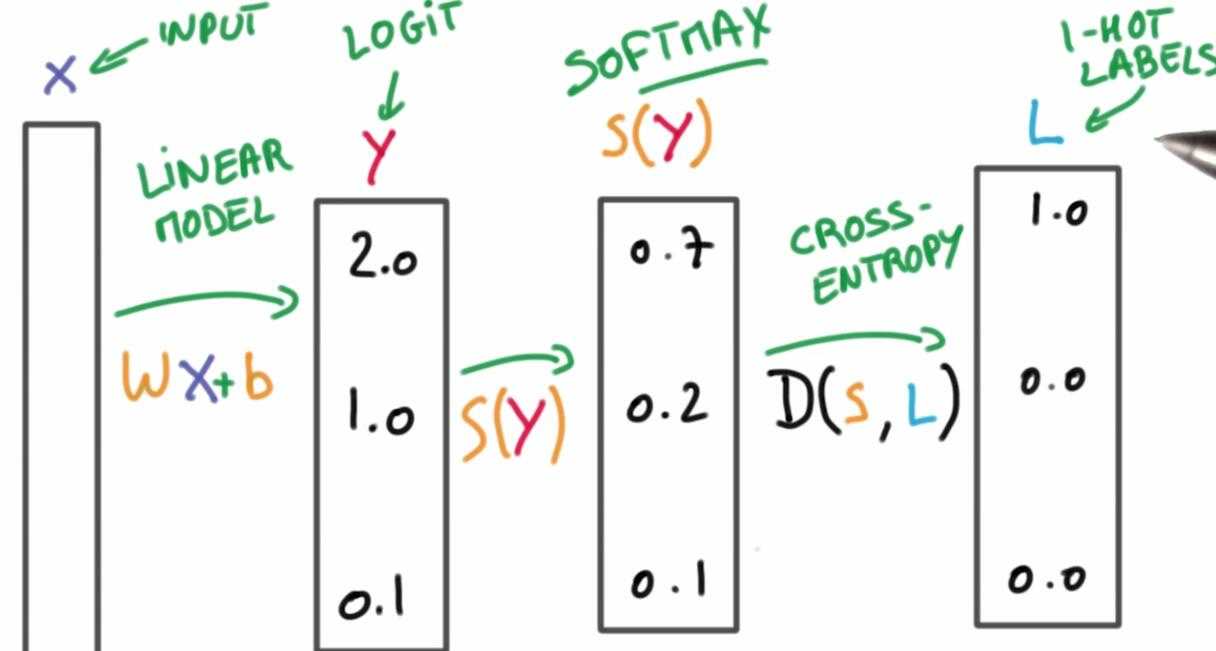同时我们将使用交叉熵损失函数来量化预测得到的分类标签的得分与真实标签之间的一致性。
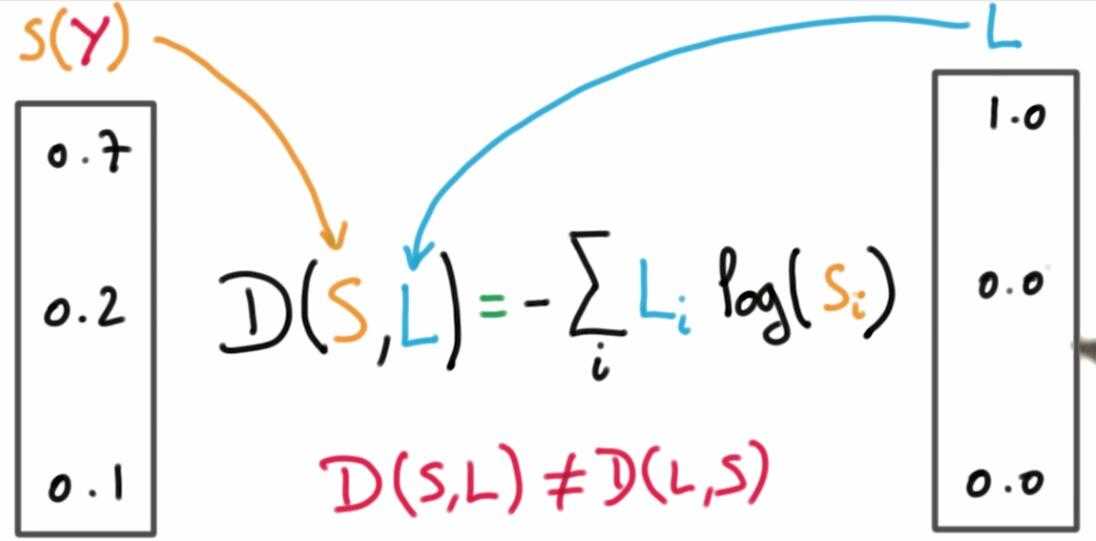即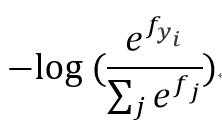 
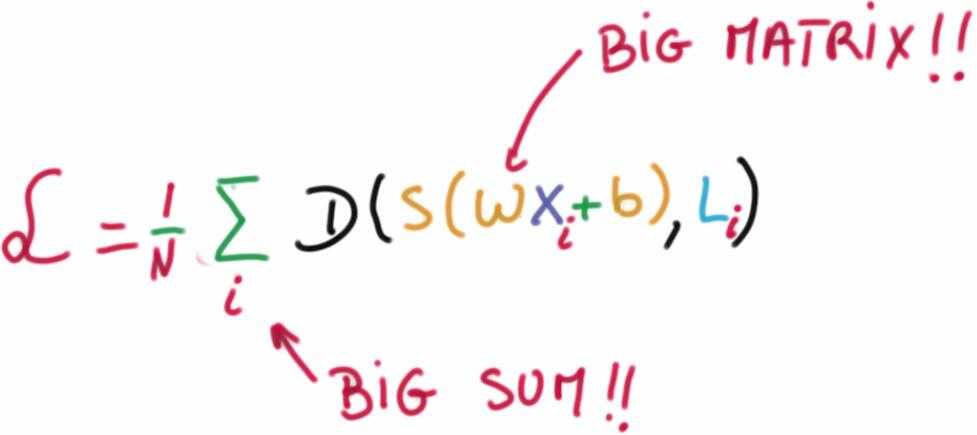我们的目的就是找到一对合适的 W 和 b 最小化损失函数。
该线性分类问题就转化成了一个数据最优化的问题，在最优化的过程中，通过更新评分函数的参数来最小化损失函数值。
最简单的方法就是梯度下降法，对损失函数的每一个变量求偏导，然后不断更新变量，直到达到局部最优。
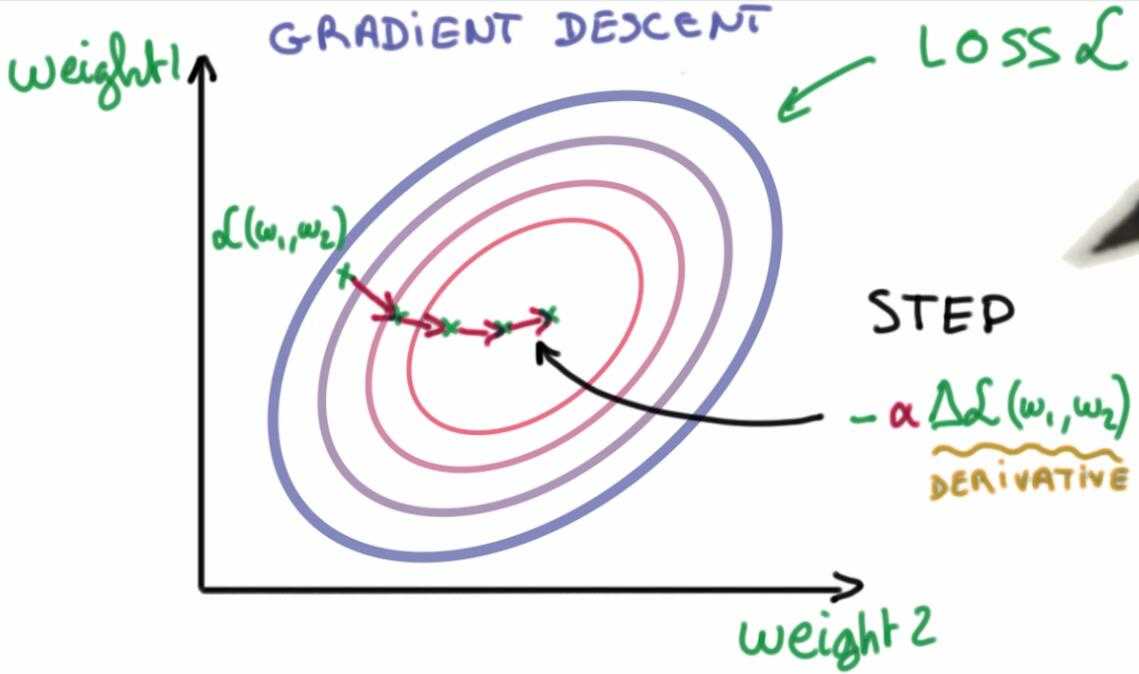
7. 正则化输入和初始权重
输入数据过大或者过小都很严重影响我们的数值计算过程，所以我们要尽量将数据正则化为均值为0同方差的数据。
以图像为例，我们可以这么做：
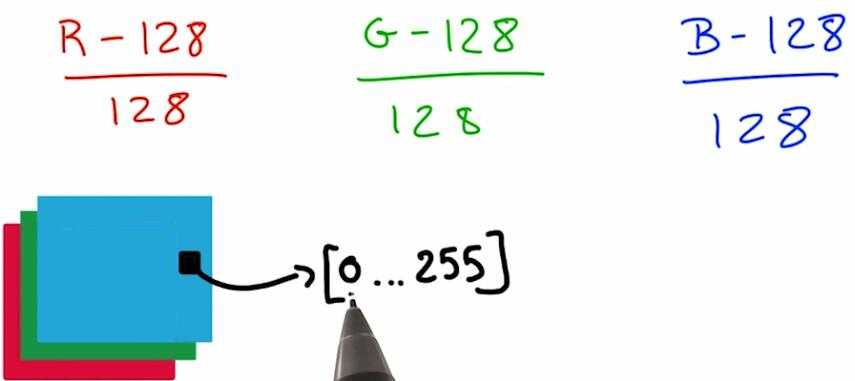
这并没有改变你的图像信息，而且更利于数值优化。
在梯度下降过程众，你也会想要你的权重 W 和偏置 b 初始化在一个足够好的开始点。
比如，我们的参数可以从均值为0，标准差为sigma 的高斯分布中随机抽取。sigma的值决定了最优化过程中，在初始点你输出的数量级，通过softmax函数后，也将决定你初始化概率分布的峰值。
一个大的sigma将决定你的初始概率分布有一个较大的峰值，一个小的sigma则使得你的概率分布是不确定的。通常比较好的是开始于一个小的不确定的分布，所以选一个小的sigma。
总结来说，我们得到我们的训练数据后，先将这些数据标准化为均值为0方差一致的数据。然后我们把他乘以 权重 W 加上偏置项 b，权重初始化为随机权重。然后我们使用softmax函数得到概率，使用交叉熵损失计算整个训练数据上的平均损失。然后我们使用神奇的最优化包计算这个损失函数对权重和偏差的倒数，接着沿导数相反方向更新权重和偏差。重复这个过程，直到损失函数达到极小值（局部最优）。
标签：均值 图片 使用 one 目标 ret 方差 oat 偏差
原文地址：http://www.cnblogs.com/xuanyuyt/p/6010917.html
