标签：home namespace 矩阵快速幂 cto blank log numbers span 斐波那契
http://acm.tzc.edu.cn/acmhome/problemdetail.do?&method=showdetail&id=3012
题意：f[1]=1,f[2]=2,f[n]=f[n-1]+f[n-2],定义：
这道题只有1s，很明显模拟的话单单指数部分的 S[ x ] 就O(n)超时了，更不用说求幂了。
而该 f[ x ] 为斐波那契数列，于是想到的是构造一个矩阵，利用矩阵来求 f[ x ] 和 S[ x ] 。
初始的构造方法是一个4*4的矩阵：
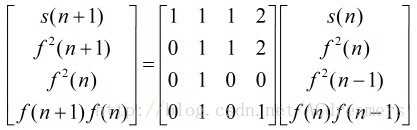
记为A[ n ]=T * B[ n-1 ]，然后可以得到 A[ n ]=T^(x-2) * B[ 2 ] ( 当 x>2 时 )
然后用矩阵快速幂的方法 求 M=T^(x-2) , 然后 s[ n ]= M[ 0 ][ 0 ]*s[ 2 ] + M[ 0 ][ 1 ] * f^2[ 2 ] + M[ 0 ][ 2 ] * f^2[ 1 ] + M[ 0 ][ 3 ] * f[ 1 ]*f[ 2 ]
然后用降幂公式 s [ x ] =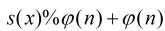 
, 其中 ψ ( n )为欧拉函数值。
降幂之后再用快速幂取模的方法 求 ans = ( a^s ) % n 求最终的答案。
不过不知道哪出问题了，一直在 WA 和 TL 中来回跑。
然后换了个构造方法，构造 2*2 的矩阵：
A[ X ] = | f[ x+1 ] f[ x ] | | 1 1 | ^(x+1)
| f[ x ] f[ x-1 ] | = | 1 0 |
会发现 S[ x ] = F[ x+1 ] * F[ x ] -1
用快速幂 将 F[ x+1 ] 和 F[ x ] 求出 则可以得到 S[ x ] 时间复杂度为O( log n )
然后再用降幂公式和快速幂取模 求 ans 为最终答案
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<algorithm>
#include<climits>
#include<sstream>
#define eps 1e-9
#define pi aocs(-1)
#define INF 0x3f3f3f3f
#define inf -INF
using namespace std;
const int maxn = 1e3 + 10;
typedef long long LL;
LL a,x,n,phi_n,F1,F2;
struct matrix{
LL m[2][2];
}p,q;
LL phi(LL n){ // 欧拉函数 s=s%phi+phi 降幂
LL res = n;
for(int i = 2;i*i<=n;++ i){
if(n%i==0){
res = res - res/i;
do{
n/=i;
}while(n%i == 0);
}
}
if(n > 1) res = res - res/n;
return res;
}
matrix multi(matrix a,matrix b,LL mod){
matrix c;
for(int i = 0;i < 2;++ i)
for(int j = 0;j < 2;++ j){
c.m[i][j] = 0;
for(int k = 0;k < 2;++ k)
c.m[i][j]+=a.m[i][k]*b.m[k][j];
c.m[i][j]%=mod;
}
return c;
}
matrix quick_mod(matrix a,LL b,LL mod){
matrix ans = p;
while(b){
if(b&1) ans = multi(ans,a,mod);
b>>=1;
a = multi(a,a,mod);
}
return ans;
}
LL quickpow_mod(LL a,LL b,LL mod){
LL res = 1;
while(b){
if(b&1) res = (res*a)%mod;
b>>=1;
a = (a*a)%mod;
}
return res;
}
void init(){
p.m[0][0] = p.m[1][1] = 1; p.m[1][0] = p.m[0][1] = 0;
q.m[0][0] = q.m[0][1] = q.m[1][0] = 1;q.m[1][1] = 0;
}
int main(){
matrix ans;
init();
while(cin>>a>>x>>n&&a+x+n){
phi_n = phi(n);
ans = quick_mod(q,x+1,phi_n);
cout<<"aaa "<<ans.m[0][0]<<ans.m[0][1]<<endl;
F1 = ((ans.m[0][0]*ans.m[0][1]-1)%phi_n + phi_n )%phi_n + phi_n;
LL res = quickpow_mod(a,F1,n);
cout<<res<<endl;
}
return 0;
}
标签：home namespace 矩阵快速幂 cto blank log numbers span 斐波那契
原文地址：http://www.cnblogs.com/fzfn5049/p/6017135.html
