标签:scanf 题目 ... else log png 开始 算法 bsp
一、实验内容
1.输入两个正整数m和n(要求m<=n), 求m!+(m+1)!+(m+2)!…+n!
#include<stdio.h> int main() { double m,n,a,b; printf("输入两个正整数m和n(m≤n),求m!+(m+1)!+...n!\n"); printf("请输入m="); scanf("%lf",&m); printf("请输入n=") ; scanf("%lf",&n); if(m>n) { printf("输入错误\n"); } else { a=1; b=0; for(m;m<=n;m=m+1) { a=a*m; b=b+a; } } printf("%.lf",b); return 0; }
2.输出1000以内的所有完数。所谓完数是指这个数恰好等于除他本身外的所有因子之和。例,6的因子为1,2,3,6=1+2+3,所以6是完数。
#include<stdio.h> int main() { int a,i,j; for(j=1;j<=1000;j=j+1) { a=0; for(i=1;i<=j-1;i=i+1) { if(j%i==0) { a=a+i; } } if(a==j) { printf("%d\n",a); } } return 0; }
3.奇偶归一猜想——对于每一个正整数,如果它是奇数,则对它乘3再加1,如果它是偶数,则对它除以2,如此循环,最终都能够得到1。 如n = 11,得序列:11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1。(共有14个步骤) 题目输入正整数n,求这个n多少步能归一
#include<stdio.h> int main() { int a,i; printf("对于一个正整数,如果它是奇数,则对它乘三再加一,如果它是偶数,则对它除以二,如此循环,最终都能得到1\n请输入一个正整数\n"); scanf("%d",&a); i=0; if(a<=0) { printf("输入错误\n"); } else { while(a!=1) { if(a%2!=0) { a=a*3+1; } else if(a%2==0) { a=a/2; } i=i+1; } printf("这个数经过了%d步能归一\n",i); } return 0; }
附加题:
1.输入一个正整数n,输出2/1+3/2+5/3+8/5+…的前n项之和,保留2位小数,该序列从第二项起,每一项的分子是前一项分子与分母的和,分母是前一项的分子。
#include<stdio.h> int main() { int n,i; double a,b,c,d,e,f; printf("输入一个正整数n,计算2/1+3/2+5/3+8/5+…的前n项之和,保留2位小数,该序列从第二项起,每一项的分子是前一项分子与分母的和,分母是前一项的分子。\n请输入\n"); scanf("%d",&n); if(n<=0) { printf("输入错误\n"); } else { d=2; e=1; f=0; for(i=0;i<n;i=i+1) { a=d; b=e; c=a/b; d=a+b; e=a; f=f+c; } printf("前%d项和为%.2lf",n,f); } return 0; }
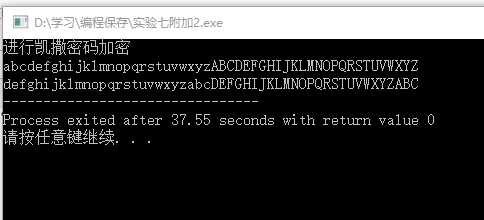
2.凯撒密码(caeser)的原理:每一个字母按字母表顺序向后移3位,如a加密后变成d,b加密后变成e,……x加密后变成a,y加密后变成b,z加密后变成c。例如:“baidu”用凯撒密码法加密后字符串变为“edlgx”。试写一个算法,将键盘输入的文本字符串(只包含a~z的字符)进行加密后输出。
#include<stdio.h> int main() { char x; printf("进行凯撒密码加密\n"); while(x!=‘\n‘) { scanf("%c",&x); if((x>=‘A‘&&x<=‘W‘)||(x>=‘a‘&&x<=‘w‘)) { x=x+3; printf("%c",x); } else if(x==‘X‘||x==‘Y‘||x==‘Z‘||x==‘x‘||x==‘y‘||x==‘z‘) { x=x-23; printf("%c",x); } } return 0; }
二、实验总结
1、int型,float型和double型的数据,储存的字节不同。
2、奇偶归一题,算好从哪一步开始是第一步,然后哪一步是最后一步。
3、附加题第一题,找规律,把数多写几个,算出用式子怎样来表示规律
标签:scanf 题目 ... else log png 开始 算法 bsp
原文地址:http://www.cnblogs.com/accelerator123/p/6020321.html