标签:容量 代码 nic eof names out 最大的 pac scanf
题意:
有n种技能,每个技能有两个属性,分别对应着物理伤害,魔法伤害,现在有m个连招,如果连续两个技能都选择同一种属性就会得到一个属性加成,否则就会丢失一些伤害,现在需要使得伤害最大化,求这个最大的伤害。
题解:
因为两个属性物理或者魔法只能选择一种属性,那么很容易就想到最小割,那么再用总伤害减去最小割就是最大的技能伤害,但是对于伤害加成和伤害丢失怎么办呢?有一种建图方式。
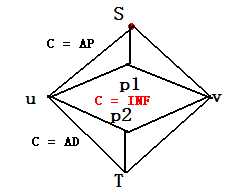
注:S 到 p1的容量是AP(魔法)加成 + 伤害丢失 , p2 到 T的容量是AD(物理)加成 + 伤害丢失。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int M = 1e6 + 7;
const int N = 1e6 + 7;
const int INF = (1 << 31) - 1;
struct edge
{
int v, c, f, nxt;
} e[M << 1];
LL sum;
int vis[N], S, T, ecnt, head[N], dep[N], cur[N], n, m;
void adde (int u, int v, int c)
{
e[ecnt] = (edge) {v, c, 0, head[u]}, head[u] = ecnt++;
e[ecnt] = (edge) {u, 0, 0, head[v]}, head[v] = ecnt++;
}
int BFS (int S)
{
queue <int> q;
q.push(S);
memset (vis, 0, sizeof vis);
vis[S] = 1, dep[S] = 0;
while (!q.empty())
{
int u = q.front();
q.pop();
for (int it = head[u]; it != -1; it = e[it].nxt)
{
int v = e[it].v;
if (!vis[v] && e[it].c > e[it].f)
{
vis[v] = 1;
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return vis[T];
}
LL DFS (int u, LL flow)
{
if (u == T || flow == 0) return flow;
LL tot = 0, F;
for (int it = cur[u]; it != -1; it = e[it].nxt)
{
cur[u] = it;
int v = e[it].v;
if (dep[u] + 1 == dep[v] && (F = DFS(v, min(flow, (LL) e[it].c - e[it].f))) > 0)
{
e[it].f += F;
e[it ^ 1].f -= F;
tot += F;
flow -= F;
if (flow == 0) break;
}
}
return tot;
}
LL dinic ()
{
LL maxf = 0;
while (BFS(S))
{
for (int i = 0; i <= T; ++ i) cur[i] = head[i];
maxf += DFS(S, INF);
}
return maxf;
}
int main ()
{
memset (head, -1, sizeof head);
scanf ("%d%d", &n, &m);
T = 2 * m + n + 1;
for (int i = 1; i <= n; ++ i)
{
int P, D;
scanf ("%d%d", &P, &D);
sum += P + D;
adde (S, i, P);
adde (i, T, D);
}
int tmp = n + 1;
for (int i = 1; i <= m; ++ i)
{
int u, v, P, D, z;
scanf ("%d%d%d%d%d", &u, &v, &D, &P, &z);
sum += P + D + z;
adde (S, tmp, P + z);
adde (tmp, u, INF);
adde (tmp, v, INF);
++tmp;
adde (u, tmp, INF);
adde (v, tmp, INF);
adde (tmp, T, D + z);
++tmp;
}
cout << sum - dinic() << endl;
return 0;
}
标签:容量 代码 nic eof names out 最大的 pac scanf
原文地址:http://www.cnblogs.com/xgtao/p/6024090.html