指数分布族与广义线性模型

标签：nat   表达   不同的   param   价格   center   ural   1.5   text   

     整理一下之前所学过的关于回归问题的思路：

• 问题引入：房屋估价，给定新的房屋信息，预测出相应的房屋价格；
• 学习过程：构建模型h(θ)；
• 线性回归：最小二乘法、梯度下降法、线性模型的概率解释；
• 局部加权回归：带权重的线性回归、权值的钟形函数；
• 逻辑回归：分类方法、梯度上升法、牛顿法、引出感知机学习算法；
• 广义线性模型：指数分布族、给定概率分布推导出线性模型。

    这一节所讨论的重点就是最后的这一条内容，回顾讨论过的线性回归与逻辑回归的假设可知：

• 在线性回归模型的概率解释中假设：

• 在逻辑回归模型的推导中假设：

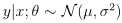
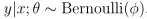
     线性回归最后一部分将会发现以上这些模型都是广义线性模型的一个特例。

一、指数分布族

     首先，要引出指数分布族的概念。它的标准表达式为：

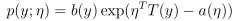
     其中，η是分布的自然参数（natural parameter）或典范参数（canonical parameter），T(y)叫做充分统计量（sufficient statistic），通常情况下T(y)=y；a(η)是对数分配函数（log partition function），而a、b与T一般都是给定的，随着η的变化，会得到不同的分布。

     下面来分别推导伯努利分布（Bernoulli distribution）与高斯分布（Gaussian distribution）的指数分不族通用表达式。

    1. 伯努利分布

      已知伯努利分布Bernoulli(Φ)，Φ为分布的均值，随着Φ的变化，可以得到不同的伯努利分布。

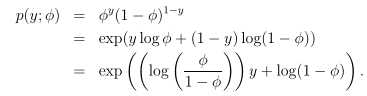
     对应标准表达式可知：

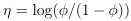
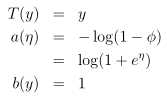
     这表明选择合适的a、b、T，可以将伯努利分布写成指数分布族的标准形式。

   2. 高斯分布

    已知高斯分布N(μ,1)，μ为分布的均值，方差对最终θ和h(θ)的选择没有影响，设置为1。

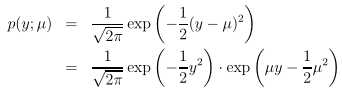
    对应标准表达式可知：

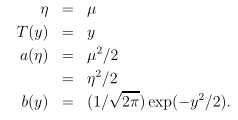
    同理，高斯分布也可以写成指数分布族的标准形式。

   3. 其他指数族分布

    还有许多其他分布属于指数分布族，如：

• 多项式分布（multinomial）
• 泊松分布（Poisson），用来对计数过程进行建模，如网站的访客数量、商店的顾客数量等；
• 伽马分布（gamma）和指数分布（exponential），用来对时间间隔进行建模，如等车时间等；
• β分布（beta）和Dirichlet分布（Dirichlet），用于概率分布；
• Wishart分布（Wishart），用于协方差矩阵分布。

 二、广义线性模型（GLM）

   1. 三个假设：

  （1）

  （2）给定x，最终的目标是要求出T(y)期望E[T(y)|x]，因为通常T(y)=y，故h(x)也可以被求出来。

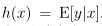
  （3）自然参数η与输入特征x呈线性相关，即

        实数时，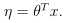  

        向量时，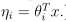 

   2. 最小二乘法：

   设定目标变量（响应变量）y是连续的，且y|x;θ服从高斯分布，由上面的推导可知η=μ，故可知假设函数h(x)为：

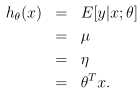
   3. 逻辑回归：

   由于考虑到二元分类问题，目标变量y取的值是0或1，很自然地就联想到可以利用伯努利分布来建立模型，假设y|x;θ服从伯努利分布Bernoulli(Φ)，所以可知它的期望为Φ：

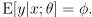
   同最小二乘法的推理过程，由伯努利分布的指数族的标准表达式可以反推出假设函数h(x)为：

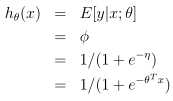
    这里还有个有趣的知识点，参数η的方程g(η)给定了分布的均值，它被叫做正则响应函数（canonical response function），而它的倒数叫做正则关联函数（canonical link function），高斯家族的正则响应函数就是判别函数（identify function），伯努利的正则响应函数就是逻辑函数（logistic function）。

指数分布族与广义线性模型

标签：nat   表达   不同的   param   价格   center   ural   1.5   text   

原文地址：http://www.cnblogs.com/wallacup/p/6024855.html