第四次作业

标签：blog   技术分享   上下限   区间   第一个   模型   长度   img   images   

5.给定如表4-9所示的概率模型，求出序列a₁a₁a₃a₂a₃a₁的实值标签。

答：由公式

解： 依题得    p(a₁)=0.2 ,p(a₂)=0.3  ,p(a₃)=0.5

       映射出    a₁=1，a₂=2，a₃=3      

 　　从概率模型可知   Fx(k)=0,k≤0,Fx(0)=0,Fx(1)=0.2,Fx(2)=0.5,Fx(3)=1,Fx(k)=1,k>3 

　　 设L⁽⁰⁾=0，u⁽⁰⁾=1

      由公式，L⁽ⁿ⁾=L^(n-1)+(U^(n-1)-L^(n-1))F_x(x_n-1) 与  u⁽ⁿ⁾=L^(n-1)+(U^(n-1)-L^(n-1))F_x(x_n) 有

当n=1(a1)时:

　　l(1)=l(0)+(u(0)-l(0))*Fx(0)=0+(1-0)*0=0

　　u(1)=l(0)+(u(0)-l(0))*Fx(1)=0+(1-0)*0.2=0.2

当n=2(a1a1)时:

　　l(2)=l(1)+(u(1)-l(1))*Fx(0)=0+(0.2-0)*0=0

　　u(2)=l(1)+(u(1)-l(1))*Fx(1)=0+(0.2-0)*0.2=0.04

当n=3(a1a1a3)是=时:

　　l(3)=l(2)+(u(2)-l(2))*Fx(2)=0+(0.04-0)*0.5=0.02 　　u(3)=l(2)+(u(2)-l(2))*Fx(3)=0+(0.04-0)*1 =0.04

当n=4(a1a1a3a2)时:

　　l(4)=l(3)+(u(3)-l(3))*Fx(1)=0.02+(0.04-0.02)*0.2=0.024

　　u(4)=l(3)+(u(3)-l(3))*Fx(2)=0.02+(0.04-0.02)*0.5 =0.03

当n=5(a1a1a3a2a3)时:

　　l(5)=l(4)+(u(4)-l(4))*Fx(2)=0.024+(0.03-0.024)*0.5=0.027 　　u(5)=l(4)+(u(4)-l(4))*Fx(3)=0.024+(0.03-0.024)*1=0.03

当n=6(a1a1a3a2a3a1)时:

　　l(6)=l(5)+(u(5)-l(5))*Fx(0)=0.027+(0.03-0.027)*0=0.027 　　u(6)=l(5)+(u(5)-l(5))*Fx(1)=0.027+(0.03-0.027)*0.2=0.0276

所以，序列a₁a₁a₃a₂a₃a₁的实值标签为：T_x(a1a1a3a2a3a1)=(0.027+0.0276)/2=0.0273

6.对于表4-9给出的概率模型，对于一个标签为0.63215699的长度为10的序列进行解码。

解：

由题可知：T_x=0.63215699，F_x(k≤0)=0,  F_x(1)=0.2, F_x(2)=0.5, F_x(3)=1, k>3.

  给定   l⁽⁰⁾=0，u⁽⁰⁾=1

公式：

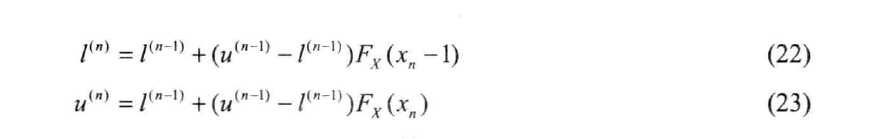
         t^*=(tag-l^(k-1))/(u^(k-1) -l^(k-1))

  F(x1)=0.2,F(x2)=0.5,F(x3)=1. 

先设u^（0）=1，l^（0）=0，则有

①解出序列的的第一个元素x₁之后的上下限为：

    l⁽¹⁾=0+(1-0)F_x(x₁-1)=F_x(x₁-1)

    u ⁽¹⁾=0+(1-0)F_x(x₁)=F_x(x₁)

如果取x₁=1,则该区间为[0,0.2)

如果取x₁=2,则该区间为[0.2,0.5)

如果取x₁=3,则该区间为[0.5,1)

因为0.63215699落入区间[0.5,1]中，所以该序列的第一个元素为a₃

②同上求出序列的的第二个元素x2的上下限为：

       l⁽²⁾=0.5+(1-0.5)F_x(x₂-1)=0.5+0.5F_x(x₂-1)

       u ⁽²⁾=0.5+(1-0.5)F_x(x₂)=0.5+0.5F_x(x₂)

如果取x₂=1,则该区间为[0.5,0.6）

如果取x₂=2,则该区间为[0.6,0.75）

如果取x₂=3,则该区间为[0.75,1）

因为0.63215699落入区间[0.6,0.75]中，所以该序列的第二个元素为a_2.

③同上求出序列的的第三个元素x3的上下限为：

        l⁽³⁾=0.6+(0.75-0.6)F_x(x₃-1)=0.6+0.15F_x(x₃-1)

        u ⁽³⁾=0.6+(0.75-0.6)F_x(x₃)=0.6+0.15F_x(x₃)

如果取x₃=1,则该区间为[0.6,0.63）

如果取x₃=2,则该区间为[0.63,0.675）

如果取x₃=3,则该区间为[0.675,0.75）

因为0.63215699落入区间[0.63,0.675]中，所以该序列的第三个元素为a_2.

④同上求出序列的的第四个元素x4的上下限为：

       l⁽⁴⁾=0.63+(0.675-0.63)F_x(x₄-1)=0.63+0.045F_x(x₄-1)

       u ⁽⁴⁾=0.63+(0.675-0.63)F_x(x₄)=0.63+0.045F_x(x₄)

如果取x₄=1,则该区间为[0.63,0.639]

如果取x₄=2,则该区间为[0.639，0.6525]

如果取x₄=3,则该区间为[0.6525,0.675]

因为0.63215699在落入[0.63,0.639]中，所以该序列的第四个元素为a_1.

⑤同上求出序列的的第五个元素x5的上下限为：

       l⁽⁵⁾=0.63+(0.639-0.63)F_x(x₅-1)=0.63+0.009F_x(x₅-1)

       u ⁽⁵⁾=0.63+(0.639-0.63)F_x(x₅)=0.63+0.009F_x(x₅)

如果取x₅=1,则该区间为[0.63,0.6318]

如果取x₅=2,则该区间为[0.6318,0.6345]

如果取x₅=3,则该区间为[0.6345,0.639]

因为0.63215699落入区间[0.6318,0.6345]中，所以该序列的第五个元素为a_2.

⑥同上求出序列的的第六个元素x6的上下限为：

       l⁽⁶⁾=0.6318+(0.6345-0.6318)F_x(x₆-1)=0.6318+0.0027F_x(x₆-1)

       u ⁽⁶⁾=0.6318+(0.6345-0.6318)F_x(x₆)=0.6318+0.0027F_x(x₆)

如果取x₆=1,则该区间为[0.6318,0.63234]

如果取x₆=2,则该区间为[0.63234,0.63315]

如果取x₆=3,则该区间为[0.63315,0.6345]

因为0.63215699落入区间[0.6318,0.63234]中，所以该序列的第六个元素为a_1.

⑦同上求出序列的的第七个元素x7的上下限为：

        l⁽⁷⁾=0.6318+(0.63234-0.6318)F_x(x₇-1)=0.6318+0.00054F_x(x₇-1)

       u ⁽⁷⁾=0.6318+(0.63234-0.6318)F_x(x₇)=0.6318+0.00054F_x(x₇)

如果取x₇=1,则该区间为[0.6318,0.631908]

如果取x₇=2,则该区间为[0.631908,0.63207]

如果取x₇=3,则该区间为[0.63207,0.63234]

因为0.63215699落入区间[0.63207,0.63234]中，所以该序列的第七个元素为a_3.

⑧同上求出序列的的第八个元素x8的上下限为：

        l⁽⁸⁾=0.63207+(0.63234-0.63207)F_x(x₈-1)=0.63207+0.00027F_x(x₈-1)

        u ⁽⁸⁾=0.63207+(0.63234-0.63207)F_x(x₈)=0.63207+0.00027F_x(x₈)

如果取x₈=1,则该区间为[0.63207,0.632124]

如果取x₈=2,则该区间为[0.632124,0.632205]

如果取x₈=3,则该区间为[0.632205,0.63234]

因为0.63215699落入区间[0.632124,0.632205]中，所以该序列的第八个元素为a_2.

⑨同上求出序列的的第九个元素x9的上下限为：

    l⁽⁹⁾=0.632124+(0.632205-0.632124)F_x(x₉-1)=0.632124+0.000081F_x(x₉-1)

    u ⁽⁹⁾=0.632124+(0.632205-0.632124)F_x(x₉)=0.632124+0.000081F_x(x₉)

如果取x₉=1,则该区间为[0.632124,0.6321402]

如果取x₉=2,则该区间为[0.0.6321402,0.6321645]

如果取x₉=3,则该区间为[0.6321645,0.63234]

因为0.63215699落入区间[0.0.6321402,0.6321645]中，所以该序列的第九个元素为a_2.

⑩同上求出序列的的第十个元素x10的上下限为：

   l⁽¹⁰⁾=0.0.6321402+(0.6321645-0.0.6321402)F_x(x₁₀-1)=0.0.6321402+0.0000243F_x(x₁₀-1)

   u ⁽¹⁰⁾=0.0.6321402+(0.6321645-0.0.6321402)F_x(x₁₀)=0.0.6321402+0.0000243F_x(x₁₀)

如果取x₁₀=1,则该区间为[0.6321402,0.63212886]

如果取x₁₀=2,则该区间为[0.63212886,0.63215325]

如果取x₁₀=3,则该区间为[0.63215325,0.6321645]

因为0.63215699落入区间[0.63215325,0.6321645]中，所以该序列的第十个元素为a_3.

所以，得到所求序列为a₃a₂a₂a₁a₂a₁a₃a₂a₂a_3。

第四次作业

标签：blog   技术分享   上下限   区间   第一个   模型   长度   img   images   

原文地址：http://www.cnblogs.com/song520-/p/6036748.html