标签:线性代数 投影 没有 概念 技术分享 自己 src 传感器 img
1.几个基本概念。
地理坐标系:北东地。北为X轴、东为Y轴、地为Z轴。
机体坐标系:见下图。
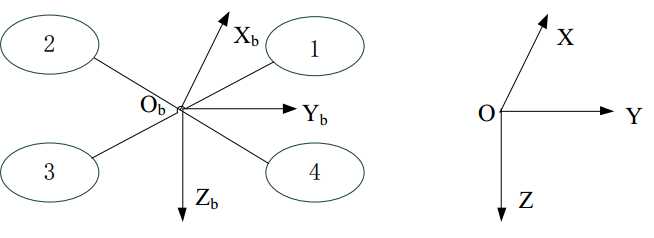
姿态角:我的理解是,roll角是Zb在ZOY平面与Z轴的夹角。pitch角是Zb在ZOX平面与Z轴的夹角。yaw角是Xb在XOY平面与X轴的夹角。
旋转矩阵:地理坐标系到机体坐标系的转换矩阵。旋转矩阵为正交阵,逆即转置。
传感器:都是基于机体坐标系的。加速度计测三轴的加速度,磁力计测三轴的磁感应强度,陀螺仪测三轴的角速度。注意角速度的定义,方向是沿着三轴的。得到姿态角主要靠陀螺仪测得的角速度积分,但存在漂移误差,因此要用加速度计和磁力计随时校正。
很重要的:在地理坐标系下,重力加速度坐标始终为(0,0,1g),磁场坐标为(M,0,D)。在地球表面,磁场始终是沿着磁感应线指北的,某点的磁场强度为磁感应线在该点的切线,它在北方有个分量,在垂直方向有个分量,在Y轴是没有分量的,即(M,0,D)。这里还有一点,地理的北极和磁场的北极是不重合的,有一定的夹角,即磁偏角。根据经纬度是可以查到这个夹角的大小的。我们定义的地理坐标系的北当然是地理的北。但用磁力计求得实际是Xb与地磁的北的夹角,我们最后会加上磁偏角,这样就是Xb与地理北的夹角了,就是真正的航向角啦。
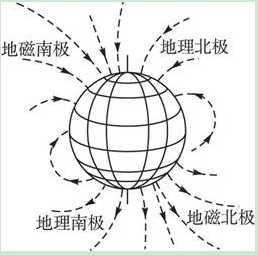
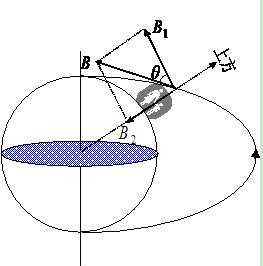
理解重力加速度和磁感应强度的概念是非常重要的。
好了,我们可以开始求初始姿态角了。
2.加速度计求roll,pitch角。
飞机静止放在放地上时,地理坐标系下重力加速度为(0,0,g),机体坐标系下加速度测量的三轴加速度为(ax,ay,az)
它们两者之间的关系是怎么表示呢,可以想象一个长方体,(ax,ay,az)是三条边,(0,0,g)是对角线。
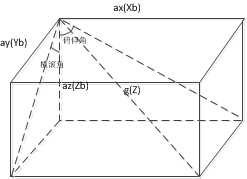
这个图可以清晰的说明一切啦。画图花了我好久。求姿态角就是求两个坐标系的夹角关系。在求俯仰角和横滚角时,我们完全可以把Z轴当做参考来求。上面我说俯仰角是Zb在XOZ平面的投影与Z轴的夹角,这里我是把Z轴投影到XbOZb平面上的,仔细想想是一样的,Z轴在XbOZb平面上的投影和Zb轴的夹角依然是俯仰角啦。横滚同理。
这样roll=arctan(ay/az),pitch =-arctan(ax/az) 方向的正负号是自己定义的。
3.磁力计求航向角。
地理坐标系下该点的磁场强度为(M,0,D),磁力计测得的三轴磁场强度为(mx,my,mz)。
当我们认为飞机是完全水平放在地上的时候,即Z轴和Zb轴是平行的时候,完全不用考虑垂直方向了。我们只用考虑XOY平面了。
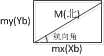
那么yaw=arctan(my/mx)
很简单对不对,但实际上飞机是不可能水平放在地面上的,肯定会有一点倾斜的,也就是说肯定会有roll和pitch角啦。只要飞机倾斜,磁力计测得的磁场强度mx就不是真正的水平X轴上的分量了,my当然也不是了。我们必须把根据mx,my,mz,roll,pitch求出投影在XOY面上的两个量了。
我们是先用加速度计求出roll和pitch角,然后根据求得的roll和pitch角,磁力计的测量的(mx,my,mz)来求yaw角。对,这才是求初始姿态角正确的打开方式。
直接按思路求出XOY上投影量比较复杂,但绝对是可以的,下面有一种比较巧妙的办法。

4.好吧,我们在这里又要讲另外一个很重要的线性代数知识。才能理解上面图片里说的什么。

根据上图可以得到一个重要结论,那就是,从机体坐标系到地理坐标系的转换矩阵的第3行的三个元素即重力加速度在机体坐标的三个分量,即地理坐标系下[0,0,g]对应机体坐标系下[ax,ay,az]!同理,磁力计的三个分量,也就是可以认为地理坐标系下[M,0,D]对应机体坐标系下[mx,my,mz]。
标签:线性代数 投影 没有 概念 技术分享 自己 src 传感器 img
原文地址:http://www.cnblogs.com/aipan-123456/p/6056814.html