标签:include math min silver 距离 sort names define ons
小 A 和小 B 决定利用假期外出旅行,他们将想去的城市从 1 到 N 编号,且编号较小的
城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 i 的海拔高度为
Hi,城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值,即
d[i,j] = |Hi− Hj|。
旅行过程中,小 A 和小 B 轮流开车,第一天小 A 开车,之后每天轮换一次。他们计划
选择一个城市 S 作为起点,一直向东行驶,并且最多行驶 X 公里就结束旅行。小 A 和小 B
的驾驶风格不同,小 B 总是沿着前进方向选择一个最近的城市作为目的地,而小 A 总是沿
着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离
相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的
城市,或者到达目的地会使行驶的总距离超出 X 公里,他们就会结束旅行。
在启程之前,小 A 想知道两个问题:
1.对于一个给定的 X=X0,从哪一个城市出发,小 A 开车行驶的路程总数与小 B 行驶
的路程总数的比值最小(如果小 B 的行驶路程为 0,此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比
值都最小,则输出海拔最高的那个城市。
总数。
第一行包含一个整数 N,表示城市的数目。
第二行有 N 个整数,每两个整数之间用一个空格隔开,依次表示城市 1 到城市 N 的海
拔高度,即 H1,H2,……,Hn,且每个 Hi都是不同的。
第三行包含一个整数 X0。
第四行为一个整数 M,表示给定 M 组 Si和 Xi。
接下来的 M 行,每行包含 2 个整数 Si和 Xi,表示从城市 Si出发,最多行驶 Xi公里。
输出格式:输出共 M+1 行。
第一行包含一个整数 S0,表示对于给定的 X0,从编号为 S0的城市出发,小 A 开车行驶
的路程总数与小 B 行驶的路程总数的比值最小。
接下来的 M 行,每行包含 2 个整数,之间用一个空格隔开,依次表示在给定的 Si和
Xi下小 A 行驶的里程总数和小 B 行驶的里程总数。
drive1 4 2 3 1 4 3 4 1 3 2 3 3 3 4 3 drive2 10 4 5 6 1 2 3 7 8 9 10 7 10 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7
drive1 1 1 1 2 0 0 0 0 0 drive2 2 3 2 2 4 2 1 2 4 5 1 5 1 2 1 2 0 0 0 0 0
【输入输出样例 1 说明】
 (图挂了)
(图挂了)
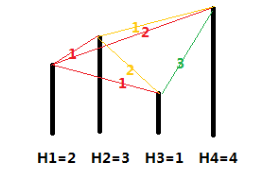
各个城市的海拔高度以及两个城市间的距离如上图所示。
如果从城市 1 出发,可以到达的城市为 2,3,4,这几个城市与城市 1 的距离分别为 1,1,2,
但是由于城市 3 的海拔高度低于城市 2,所以我们认为城市 3 离城市 1 最近,城市 2 离城市
1 第二近,所以小 A 会走到城市 2。到达城市 2 后,前面可以到达的城市为 3,4,这两个城
市与城市 2 的距离分别为 2,1,所以城市 4 离城市 2 最近,因此小 B 会走到城市 4。到达城
市 4 后,前面已没有可到达的城市,所以旅行结束。
如果从城市 2 出发,可以到达的城市为 3,4,这两个城市与城市 2 的距离分别为 2,1,由
于城市 3 离城市 2 第二近,所以小 A 会走到城市 3。到达城市 3 后,前面尚未旅行的城市为
4,所以城市 4 离城市 3 最近,但是如果要到达城市 4,则总路程为 2+3=5>3,所以小 B 会
直接在城市 3 结束旅行。
如果从城市 3 出发,可以到达的城市为 4,由于没有离城市 3 第二近的城市,因此旅行
还未开始就结束了。
如果从城市 4 出发,没有可以到达的城市,因此旅行还未开始就结束了。
【输入输出样例 2 说明】
当 X=7 时,
如果从城市 1 出发,则路线为 1 -> 2 -> 3 -> 8 -> 9,小 A 走的距离为 1+2=3,小 B 走的
距离为 1+1=2。(在城市 1 时,距离小 A 最近的城市是 2 和 6,但是城市 2 的海拔更高,视
为与城市 1 第二近的城市,所以小 A 最终选择城市 2;走到 9 后,小 A 只有城市 10 可以走,
没有第 2 选择可以选,所以没法做出选择,结束旅行)
如果从城市 2 出发,则路线为 2 -> 6 -> 7 ,小 A 和小 B 走的距离分别为 2,4。
如果从城市 3 出发,则路线为 3 -> 8 -> 9,小 A 和小 B 走的距离分别为 2,1。
如果从城市 4 出发,则路线为 4 -> 6 -> 7,小 A 和小 B 走的距离分别为 2,4。
如果从城市 5 出发,则路线为 5 -> 7 -> 8 ,小 A 和小 B 走的距离分别为 5,1。
如果从城市 6 出发,则路线为 6 -> 8 -> 9,小 A 和小 B 走的距离分别为 5,1。
如果从城市 7 出发,则路线为 7 -> 9 -> 10,小 A 和小 B 走的距离分别为 2,1。
如果从城市 8 出发,则路线为 8 -> 10,小 A 和小 B 走的距离分别为 2,0。
全国信息学奥林匹克联赛(NOIP2012)复赛
提高组 day1
第 7 页 共 7 页
如果从城市 9 出发,则路线为 9,小 A 和小 B 走的距离分别为 0,0(旅行一开始就结
束了)。
如果从城市 10 出发,则路线为 10,小 A 和小 B 走的距离分别为 0,0。
从城市 2 或者城市 4 出发小 A 行驶的路程总数与小 B 行驶的路程总数的比值都最小,
但是城市 2 的海拔更高,所以输出第一行为 2。
【数据范围】
对于 30%的数据,有 1≤N≤20,1≤M≤20;
对于 40%的数据,有 1≤N≤100,1≤M≤100;
对于 50%的数据,有 1≤N≤100,1≤M≤1,000;
对于 70%的数据,有 1≤N≤1,000,1≤M≤10,000;
对于100%的数据,有1≤N≤100,000,1≤M≤10,000,-1,000,000,000≤Hi≤1,000,000,000,
0≤X0≤1,000,000,000,1≤Si≤N,0≤Xi≤1,000,000,000,数据保证 Hi互不相同。
NOIP 2012 提高组 第一天 第三题
看懂题意就需要20分钟的样子。
倍增处理出从某个城市出发,走多少轮之后的消费,然后枚举每个城市作为出发点计算最优解即可。
↑思路还好理解,写出来超长
1 /*by SilverN*/ 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<set> 8 #include<map> 9 #define LL long long 10 using namespace std; 11 const LL INF=1e13; 12 const int mxn=100010; 13 int read(){ 14 int x=0,f=1;char ch=getchar(); 15 while(ch<‘0‘ || ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} 16 while(ch>=‘0‘ && ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} 17 return x*f; 18 } 19 map<LL,int>mp; 20 set<LL>st; 21 int n; 22 int h[mxn]; 23 int wa[mxn],wb[mxn];//[i]位置a开车花费和b开车花费 24 int fa[mxn],fb[mxn];//[i]位置a,b开车去向的结点 25 struct DIR{LL a,b;int v;}dir[mxn][17];//倍增数组 26 //bas 27 struct dist{LL h,dis;}t[5]; 28 inline int cmp(dist a,dist b){ 29 if(a.dis!=b.dis)return a.dis<b.dis; 30 return a.h<b.h; 31 } 32 double calc(int x,int lim,bool mode){//mode0:求比例 mode1:求方案 33 int a=0,b=0; 34 for(int i=16;i>=0;i--) 35 if(dir[x][i].v && a+b+dir[x][i].a+dir[x][i].b<=lim){ 36 a+=dir[x][i].a;b+=dir[x][i].b; 37 x=dir[x][i].v; 38 } 39 if(!mode){ 40 printf("%d %d\n",a,b); 41 return 0; 42 } 43 else return b==0?INF:(double)a/(double)b; 44 } 45 void solve1(){//求比例 46 double mini=1e20;int ans=0; 47 int lim=read(); 48 for(int i=1;i<=n;i++){ 49 double res=calc(i,lim,1); 50 if(res<mini || (res==mini && h[i]>h[ans]) )mini=res,ans=i; 51 } 52 printf("%d\n",ans); 53 return; 54 } 55 void solve2(){//计算方案 56 int m=read(); 57 int x,lim; 58 for(int i=1;i<=m;i++){ 59 x=read();lim=read(); 60 calc(x,lim,0); 61 } 62 return; 63 } 64 int main(){ 65 n=read(); 66 int i,j; 67 for(i=1;i<=n;i++){ 68 h[i]=read(); 69 mp[h[i]]=i;//离散化 70 } 71 st.insert(INF);st.insert(-INF); 72 for(i=n;i;i--){ 73 st.insert(h[i]); 74 t[1].h=*--st.lower_bound(h[i]); 75 t[2].h=*st.upper_bound(h[i]); 76 if(t[1].h!=-INF) 77 t[3].h=*--st.lower_bound(t[1].h); 78 else t[3].h=-INF; 79 if(t[2].h!=-INF) 80 t[4].h=*st.upper_bound(t[2].h); 81 else t[4].h=INF; 82 for(j=1;j<=4;j++) 83 t[j].dis=abs(t[j].h-h[i]); 84 sort(t+1,t+5,cmp); 85 //统计最近和次近城市 86 wa[i]=t[2].dis;fa[i]=mp[t[2].h];//A开车的去向 87 wb[i]=t[1].dis;fb[i]=mp[t[1].h];//B开车的去向 88 if(!fa[i])continue; 89 dir[i][0].a=wa[i]; 90 dir[i][0].v=fa[i]; 91 if(!fb[fa[i]])continue; 92 dir[i][1].a=wa[i];dir[i][1].b=wb[fa[i]]; 93 dir[i][1].v=fb[fa[i]]; 94 for(j=2;j<=16;j++){ 95 if(!dir[dir[i][j-1].v][j-1].v)break; 96 dir[i][j].a=dir[i][j-1].a+dir[dir[i][j-1].v][j-1].a; 97 dir[i][j].b=dir[i][j-1].b+dir[dir[i][j-1].v][j-1].b; 98 dir[i][j].v=dir[dir[i][j-1].v][j-1].v; 99 } 100 }//预处理AB在每个城市的移动方向和代价 101 solve1(); 102 solve2(); 103 return 0; 104 }
标签:include math min silver 距离 sort names define ons
原文地址:http://www.cnblogs.com/SilverNebula/p/6059417.html