数据结构：二叉树的链式存储

标签：src   c语言版   中序遍历   nbsp   指针   eof   code   中序   链式存储   

数据结构：二叉树的链式存储（C语言版）

 1.写在前面

　　二叉树同样有两种存储方式，数组和链式存储，对于数组来说，我们利用二叉树的性质然后利用下标可以方便的找到一个节点的子节点和父节点。

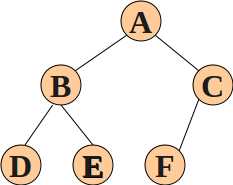
二叉树的性质:
　　1.二叉树的第i层上至多有2^i-1个节点
　　2.深度为K的二叉树至多有2^k-1个节点
　　3.任何一个二叉树中度数为2的节点的个数必度数为0的节点数目少1.
　　　　说明:度数为0,为叶子节点。
　　4.具有n个节点的完全二叉树的深度为|_Log₂N_|+1
　　5.若完全二叉树中的某节点编号为i，则若有左孩子编号为2i，若有右孩子编号为2i+1，母亲节点为i/2。

　　结合第5条性质，可以在这种完全二叉树中十分方便的找到任何相关联(父子、兄弟等)的元素。

　　但是由于顺序存储天生适配于完全二叉树，对于下面这种非完全二叉树并不合适，所以我们需要用到另一种存储方式——链式存储。

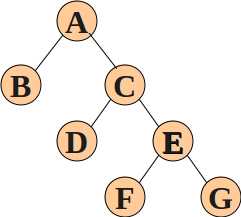
　　在链式存储中，每个节点的结构如下

　　一个存储数据的变量与两个指向孩子的指针域。
　　利用指针域我们便可以完美的存储非完全二叉树，如下：

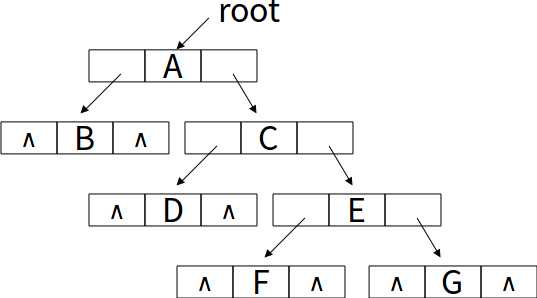
2.代码分解

?首先根据上述图示，我们不难给出节点的描述

typedef struct BiTNode
{
    TElemType data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

?创建和遍历链式二叉树
　　　　创建二叉树并不是十分容易的，因为它的创建方式也对应三种顺序，其实我认为二叉树的遍历和二叉树的创建可以说是几乎一样的过程。无非是创建的过程是给data赋值，遍历是取出data。
　　我们先不给出创建的代码，而是要明白：

说明：

　　1.叶子节点不是没有左右孩子，只不过左右孩子都是空。
　　2.我们在手动创建的过程中要根据层数来判断叶子节点左右空孩子的个数！
　　3.创建和遍历的执行顺序是一样的，那么输入和取出的值才会是一样的。

　　比如我们要先序创建一个上述图片中的二叉树，我们应该怎样输入呢？
　　　　AB##CD##EF##G##

　# 在这里是表示叶子节点的左右节点为空。

　　代码如下：

void createBitree(Bitree &T)
{
    char ch;
    if((ch=getchar())==‘#‘)
        T=NULL;
    else
    {
        T=(Bitnode*)malloc(sizeof(Bitnode));
        T->data=ch;
        createBitree(T->Lchild);
        createBitree(T->Rchild);
    }
}                

/*先序遍历*/
void preTraverse(Bitree T)
{
    if(T!=NULL)
    {
        printf("%c",T->data);
        preTraverse(T->Lchild);
        preTraverse(T->Rchild);
       }
}

/*中序遍历*/
void  inorder(Bitree T)
{
    if(T!=NULL)
    { 
        inorder(T->Lchild); 
        printf("%c",T->data);
        inorder(T->Rchild);
    } 
}    

/*后序遍历*/
void  postorder(Bitree T)
{
       
if(T!=NULL)
{
postorder(T->lchild);
postorder(T->rchild);
printf("%c",T->data);
      }
}

?我们输入字符后三种遍历情况如下：
　　AB##CD##EF##G##
　　　　ABCDEFG
　　　　BADCFEG
　　　　BDFGECA
?求二叉树的深度

int   Depth(Bitree T)
{//返回深度
    int d,dl,dr;
    if(!T)
        d=0;
    else {
        dl=Depth(T->Lchild);
        dr=Depth(T->Rchild);
        d=1+(dl>dr?dl:dr) ;
    }

    return d;
}

数据结构：二叉树的链式存储

标签：src   c语言版   中序遍历   nbsp   指针   eof   code   中序   链式存储   

原文地址：http://www.cnblogs.com/MrSaver/p/6059918.html