标签:运算符 priority 数组 string 开始 ptr png 项目 math
为了可以出带括号的题目,我学习了以往同学的作业。庆幸的是出题的要求只是出四个数进行运算就行,这样就大大缩减了这个功能的难度。
只有一对括号出现可以有以下几种情况:
1+1+1+1;
(1+1)+1+1;
(1+1+1)+1;
1+(1+1)+1;
1+(1+1+1);
1+1+(1+1);
所以在主类中编写了swich(i),这里的 i 是1-6的随机数,将会在上述的六种情况中随机挑选出一种。想利用这个中方法出带括号的题目,把原式从String数组类型改为String类型。
1 String zhongshi = ""; 2 int i = 0; 3 i = (int)(Math.random()*6)+1; 4 switch(i) 5 { 6 7 case 1: 8 zhongshi = "("+String.valueOf(y1)+sym1+String.valueOf(y2)+")"+sym2+String.valueOf(y3)+sym3+String.valueOf(y4); 9 break; 10 case 2: 11 zhongshi = "("+String.valueOf(y1)+sym1+String.valueOf(y2)+sym2+String.valueOf(y3)+")"+sym3+String.valueOf(y4); 12 break; 13 case 3: 14 zhongshi = String.valueOf(y1)+sym1+"("+String.valueOf(y2)+sym2+String.valueOf(y3)+")"+sym3+String.valueOf(y4); 15 break; 16 case 4: 17 zhongshi = String.valueOf(y1)+sym1+"("+String.valueOf(y2)+sym2+String.valueOf(y3)+sym3+String.valueOf(y4)+")"; 18 break; 19 case 5: 20 zhongshi = String.valueOf(y1)+sym1+String.valueOf(y2)+sym2+"("+String.valueOf(y3)+sym3+String.valueOf(y4)+")"; 21 break; 22 case 6: 23 zhongshi = String.valueOf(y1)+sym1+String.valueOf(y2)+sym2+String.valueOf(y3)+sym3+String.valueOf(y4); 24 25 }
为此,我将原来中缀遍历的转换后缀遍历的函数toback形参类型换成了String,这样的变化使得原来遍历字符串数组的方法不能用了,于是在网上找到了String类型下substring(int a,int b)方法。这个可以实现这样一种功能。从字符串的第一位开始记数,第一位记零,substring(int a,int b)是从a开始(这里a指的不是第几位,而是下标序号,从零开始),到b之前截止(这里的b也是指下标,而且不算b),截取原字符串。通过这个方法就可以遍历字符串的每个字符。最后通过获取操作符栈的大小,FOR循环将每个字符相加得到字符串类型的后缀表达式。
1 public String toback(String pre){ 2 3 String bottom = "#"; 4 5 Stack<String> OPTR = new Stack(); //运算符栈 6 Stack<String> OPND = new Stack(); //数据栈 7 8 OPTR.push(bottom); // 首先把结束标志‘#’放入栈底 9 10 for(int k=0;k<pre.length();k++) 11 { 12 if(isNum(pre.substring(k,k+1))) // 遇到数直接写入后缀表达式 13 { 14 OPND.push(pre.substring(k,k+1)); 15 } 16 else if(pre.substring(k,k+1).equals("(")) // 遇到“(”不用比较直接入栈 17 OPTR.push(pre.substring(k,k+1)); 18 else if(pre.substring(k,k+1).equals(")")) // 遇到右括号将其对应左括号后的操作符(操作符栈中的)全部写入后缀表达式 19 { 20 while(!OPTR.peek().equals("(")) 21 { 22 OPND.push( OPTR.peek()); 23 OPTR.pop(); 24 } 25 OPTR.pop(); // 将“(”出栈,后缀表达式中不含小括号 26 } 27 else if (isoperator(pre.substring(k,k+1))) 28 { 29 while(!OPTR.empty() && priority(pre.substring(k,k+1)) <= priority(OPTR.peek())) 30 { 31 // 当前的操作符小于等于栈顶操作符的优先级时,将栈顶操作符写入到后缀表达式,重复此过程 32 OPND.push(OPTR.peek()); 33 OPTR.pop(); 34 } 35 OPTR.push(pre.substring(k,k+1));// 当前操作符栈为空或者当前操作符优先级大于栈顶操作符的优先级,将该操作符入栈 36 } 37 38 39 40 41 } 42 while(OPTR.peek() != "#") // 将所有的操作符加入后缀表达式 43 { 44 OPND.push(OPTR.peek()); 45 OPTR.pop(); 46 } 47 OPTR.pop(); 48 49 //利用操作符栈逆序即可得到后缀表达式 50 while(!OPND.empty()) 51 { 52 OPTR.push(OPND.peek()); 53 OPND.pop(); 54 } 55 //后缀表达式的的存储数组 56 String back = ""; 57 int j = OPTR.size(); 58 for(int i = 0; i<j;i++) 59 { 60 61 back+=OPTR.peek(); 62 OPTR.pop(); 63 64 } 65 //将String数组转换成字符串 66 67 return back; 68 69 70 }
运行结果:
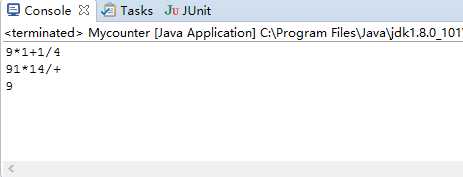
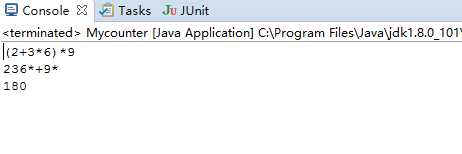
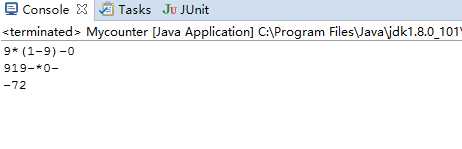
第八周(11.11-11.17)----结对项目----实现任意位置加一对括号
标签:运算符 priority 数组 string 开始 ptr png 项目 math
原文地址:http://www.cnblogs.com/YangXiaomoo/p/6060269.html