标签:优化 复杂度 creat round 长度 重复 分享 区间 code
数据结构:静态查找表(C语言版)
1.写在前面
?从查找说起:
在英汉字典中查找某个英文单词的中文解释;在新华字典中查找某个汉字的读音、含义;在对数表、平方根表中查找某个数的对数、平方根;邮递员送信件要按收件人的地址确定位置等等。
从计算机、计算机网络中查找特定的信息,就需要在计算机中存储包含该特定信息的表。查找是许多程序中最消耗时间的一部分。因而,一个好的查找方法会大大提高运行速度。
?先讨论静态查找表:
静态查找表应该是查找中最为简单的。仅仅是在固定的表中对元素的查找,而不涉及修改表中的元素。
我们讨论的是 在无序表、顺序表中的遍历查找和快速的折半查找。
2.代码分解
?无序表上的顺序查找
方式:从查找表的一端依序与表中的元素进行比较。

代码是很简单的,直接给出,以便后续分析:
#include <iostream> typedef int KeyType; typedef struct { KeyType key; int info; }ElemType; typedef struct { ElemType *elem; // 数据元素存储空间基址,建表时 int length; // 表的长度 } SSTable; int Sq_search(SSTable ST, KeyType key) { // 在无序表中查找元素key,查找成功时,返回元素在表中的位置 ,否则返回0 int i=ST.length; while (i>=1&&ST.elem[i].key!=key) i--; return i; } int Init_search(SSTable &ST,int length)//初始化表 { ST.length=length; ST.elem = (ElemType *)malloc(sizeof(ElemType)*(length+1)); } int Creat_search(SSTable &ST,int length)//创建表 { ElemType *ptr = ST.elem; int temp =0; int i=0; ptr++; //我们将第一个元素空出来! while (temp!=-1&&(i++)<length) { scanf("%d",&temp); ptr++->key=temp; } } int main() { SSTable table; Init_search(table,5); Creat_search(table,5); printf("已经找到位置:%d",Sq_search(table, 13)); return 0; }
|说明:
请注意,我们在0号位置留空,在这里仅仅是为了直观显示索引位置!
但是我们还可以优化这段代码,那就是设置监视哨。
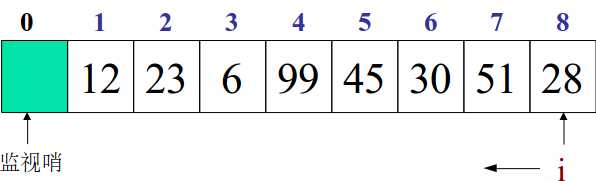
所谓监视哨,就是将空出来的下标为0的这个元素的值设为Key.
分析:
这样我们就不用多次判断i是否越界,因为就算静态表中找不到,也会在0位置上配对成功,返回0!
while (i>=1&&ST.elem[i].key!=key) i--; 改为: ST.elem[0].key = key; //监视哨:下标为0的位置存放待查找的元素 while (ST.elem[i].key!=key)
我们来分析一下算法复杂度:
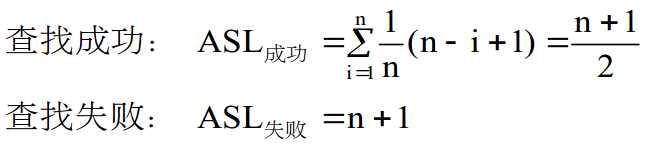
?有序表上的顺序查找
方式:在有序表上查找的时候,我们可以对无序查找进行优化:
int i = ST.length; ST.elem[0].key = key; while (key < ST.elem[i].key) i--; if (key == ST.elem[i].key) return i; return 0
即当ST.elem[i].key<= ST.elem[0].key 的时候我们就停止查找!
为什么呢?因为ST.elem[i].key<= ST.elem[0].key的时候是两种可能,要么小于,既然<就无须再比了,要是=也就得出结果了!
?有序表上的折半查找
方法:
我们把要查找的值x与数组的中间值mid进行比较,如果说x<mid,那么因为数组有序,mid右边的数字都会大于x,所以去mid右边查找是徒劳的。此时我们仅仅需要去mid左边查找即可!同理我们把mid左边也看成是一个数组,我们就可以重复上述操作了!
总之,先确定待查记录所在的范围(区间),若待查记录等于表中间位置上的记录,则查找成功;否则,缩小查找范围,即若待查记录小于中间位置上的元素,则下一次到前半区间进行查找,若待查记录大于中间位置上的元素,则下一次到后半区间进行查找。
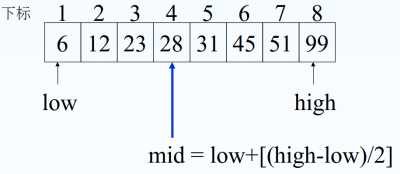
核心代码如下:
while (low<=high) { int mid= low + [(high-low)/2]; if (ST.elem[mid].key==key) return mid; //查找成功 else if (key < ST.elem[mid].key) high=mid-1; //下一次到前半区间查找 else low=mid+1; //下一次到后半区间查找 }
我们分析一下这个结束条件: while(low<=high)
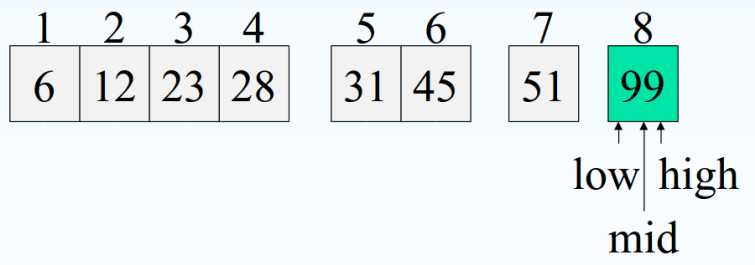
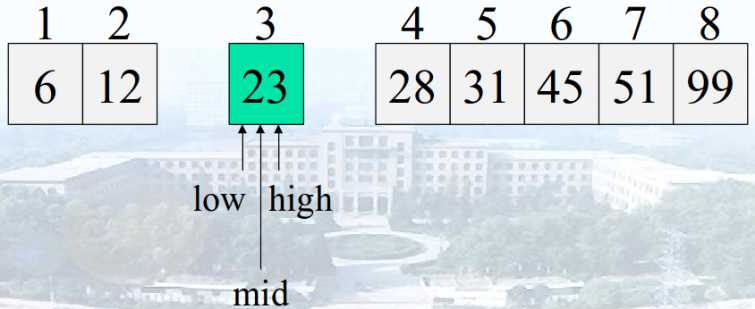
当low=high的时候,我们已经可以确定这是能够进行比较的最后一个元素了,因为此时不可能再对数组进行左右划分!
如果此时,mid元素不等于Key的话,可以判定查找失败!
若此时mid<key,low+1就会大于hi
若此时mid>key,hi-1就会小与low所以自然就会结束循环!
标签:优化 复杂度 creat round 长度 重复 分享 区间 code
原文地址:http://www.cnblogs.com/MrSaver/p/6071609.html