标签:import sof .sh 准确率 example 开始 color div alt
代码1如下:
#深度学习入门课程之感受神经网络(上)代码解释: import numpy as np import matplotlib.pyplot as plt #matplotlib是一个库,pyplot是其中一个模块 #%matplotlib inline 适用于在ipython notebook中进行绘图内嵌说明,由于我在Pycharm上写的,应此不需要这条以及下面的几个命令 plt.rcParams[‘figure.figsize‘] = (10.0,8.0) #创建一个10*8大小的绘图对象 plt.rcParams[‘image.interpolation‘] = ‘nearest‘ plt.rcParams[‘image.cmap‘] = ‘gray‘ #%load_ext autoreload #%autoreload 2 np.random.seed(0) #用于指定随机数生成时所用算法开始的整数值,如果使用相同的seed值,则每次生成的随机数相同 N = 100 #每类有一百个点 D = 2 #每个点是二维的,即x和y值为样本的特征向量 K = 3 #总共有三类,因此总共三百个训练样本 X = np.zeros((N*K,D)) #生成一个300*2的零矩阵 y = np.zeros(N*K,dtype=‘uint8‘) #生成一个1*300的零矩阵,类型为uint8 for j in xrange(K): #j从0到2 ix = range(N*j,N*(j+1)) r = np.linspace(0.0,1,N) #radius t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 #theta X[ix] = np.c_[r*np.sin(t),r*np.cos(t)] y[ix] = j #给300个点分类,每一百一类,即[0,99]为0类,[100,199]为1类,以此类推 fig = plt.figure() plt.scatter(X[:,0],X[:,1],c=y,s=40,cmap=plt.cm.Spectral) #scatter画散点图; plt.xlim([-1,1]) plt.ylim([-1,1]) #使用单层神经网络,未使用激活函数,即线性分类 w = 0.01*np.random.randn(D,K) #权值初始化,2*3,即输入两个特征向量,输出三个类别,[-0.01,0.01] b = np.zeros((1,K)) #阈值初始化,1*3的零矩阵 step_size = 1e-0 #学习步长为1 reg = 1e-3 #正则化系数,10的负三次方 num_examples = X.shape[0] #X是300*2,shape[0]求它第一维的长度即样本个数 for i in xrange(200): #迭代两百次 scores = np.dot(X,w)+b #下面是softmax分类器解释,scores为300*3 exp_score = np.exp(scores) #为300*3 probs = exp_score/np.sum(exp_score,axis = 1,keepdims = True) #每个点分类的得分所占概率(包括正确分类和错误分类),#300*3 corect_logprobs = -np.log(probs[range(num_examples),y]) #probs[range(num_examples),y]是正确分类的概率 data_loss = np.sum(corect_logprobs)/num_examples reg_loss = 0.5*reg*np.sum(w*w) #正则化项 loss = data_loss+reg_loss if i%10 == 0: #每迭代10次输出一次Loss值 print ‘iteration %d:loss %f‘%(i,loss) dscores = probs dscores[range(num_examples),y] -= 1 #Loss关于scores的偏导,为probs-1 dscores /= num_examples dW = np.dot(X.T,dscores) #data_loss传递下来的梯度 db = np.sum(dscores,axis = 0,keepdims = True) dW +=reg*w #再加上正则化项传递下来的梯度 w += -step_size * dW b += -step_size * db #求一下分类的准确率 scores = np.dot(X,w)+b predicted_class = np.argmax(scores , axis=1) #predicted_class为[1,300],为每个点得分最大的所在的那个列数,即类 print ‘training accuracy:%.2f‘%(np.mean(predicted_class == y)) #mean()是求均值 #画出分类效果 h=0.02 x_min , x_max = X[:,0].min() - 1, X[:,0].max() + 1 y_min , y_max = X[:,1].min() - 1, X[:,1].max() +1 xx, yy = np.meshgrid(np.arange(x_min , x_max ,h), np.arange(y_min , y_max ,h)) Z = np.dot(np.c_[xx.ravel(),yy.ravel()],w) + b Z = np.argmax(Z,axis = 1) Z = Z.reshape(xx.shape) fig = plt.figure() plt.contourf(xx,yy,Z,cmap=plt.cm.Spectral,alpha=0.8) plt.scatter(X[:,0],X[:,1],c=y,s=40,cmap=plt.cm.Spectral) plt.xlim(xx.min(),xx.max()) plt.ylim(yy.min(),yy.max()) plt.show()
迭代两百次,loss值到后面开始趋于饱和,accuracy为0.49,可见这种单层的神经网络和线性分类得到的最终效果并不好,效果图如下:
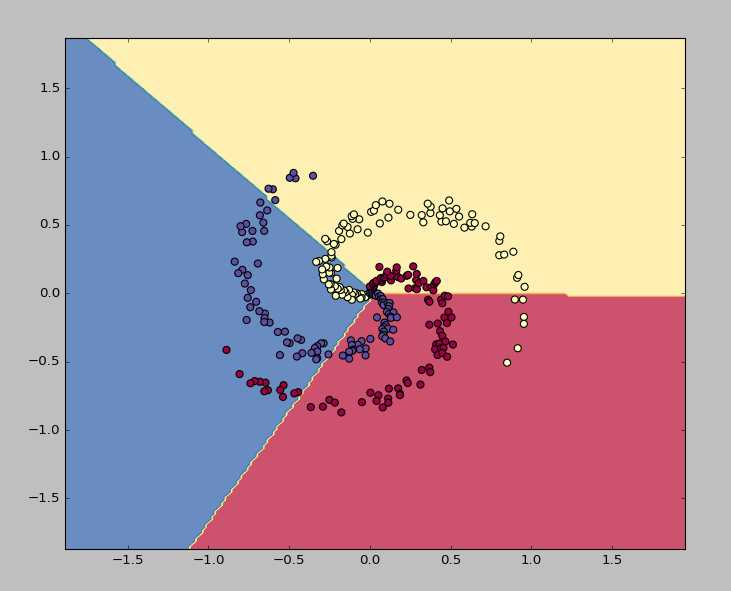
下面我们来使用双层神经网络和relu激活函数来进行非线性分类,代码如下:
#深度学习入门课程之感受神经网络(下)代码解释: import numpy as np import matplotlib.pyplot as plt #matplotlib是一个库,pyplot是其中一个模块 #%matplotlib inline 适用于在ipython notebook中进行绘图内嵌说明 plt.rcParams[‘figure.figsize‘] = (10.0,8.0) #创建一个10*8大小的绘图对象 plt.rcParams[‘image.interpolation‘] = ‘nearest‘ plt.rcParams[‘image.cmap‘] = ‘gray‘ #%load_ext autoreload #%autoreload 2 np.random.seed(0) #用于指定随机数生成时所用算法开始的整数值,如果使用相同的seed值,则每次生成的随机数相同 N = 100 #每类有一百个点 D = 2 #每个点是二维的 K = 3 #总共有三类 X = np.zeros((N*K,D)) #生成一个300*2的零矩阵 y = np.zeros(N*K,dtype=‘uint8‘) #生成一个1*300的零矩阵,类型为uint8 for j in xrange(K): #j从0到K-1 ix = range(N*j,N*(j+1)) r = np.linspace(0.0,1,N) #radius t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 #theta X[ix] = np.c_[r*np.sin(t),r*np.cos(t)] y[ix] = j #给300个点分类,每一百一类; fig = plt.figure() plt.scatter(X[:,0],X[:,1],c=y,s=40,cmap=plt.cm.Spectral) #scatter画散点图; plt.xlim([-1,1]) plt.ylim([-1,1]) #使用双层神经网络,使用Relu激活函数,将之前的线性分类变为非线性分类 h = 100 #隐层神经元个数 w = 0.01*np.random.randn(D,h) #D为输入层神经元个数 b = np.zeros((1,h)) w2 = 0.01*np.random.randn(h,K) #K为输出层神经元个数 b2 = np.zeros((1,K)) step_size = 1e-0 #学习步长为1 reg = 1e-3 #正则化系数,10的负三次方 num_examples = X.shape[0] #由于X是300*3矩阵,这里的shape[0]读取它第一维长度及300为样本个数 for i in xrange(10000): #迭代两百次 hidden_layer = np.maximum(0,np.dot(X,w)+b) #ReLu激活函数,hidden_layer为300*100 scores = np.dot(hidden_layer,w2) + b2 exp_scores = np.exp(scores) probs = exp_scores / np.sum(exp_scores,axis=1,keepdims=True) corect_logprobs = -np.log(probs[range(num_examples),y]) data_loss = np.sum(corect_logprobs) / num_examples reg_loss = 0.5*reg*np.sum(w*w) + 0.5*reg*np.sum(w2*w2) loss = data_loss + reg_loss if i%10 == 0: #每迭代10次输出一次Loss值 print ‘iteration %d:loss %f‘%(i,loss) dscores = probs dscores[range(num_examples), y] -= 1 # Loss关于scores的偏导,为probs-1 dscores /= num_examples dw2 = np.dot(hidden_layer.T,dscores) db2 = np.sum(dscores,axis=0,keepdims=True) dhidden = np.dot(dscores,w2.T) #梯度的反向传播,dihidden是300*100 dhidden[hidden_layer <= 0] = 0 #hidden_layer是隐层的输出值,若隐层输出为0,则对应位置的dhidden梯度为0不传播 dw = np.dot(X.T,dhidden) db = np.sum(dhidden,axis=0,keepdims=True) dw2 += reg * w2 dw += reg * w w += -step_size * dw w2+= -step_size * dw2 b += -step_size * db b2 += -step_size * db2 #求一下准确率 hidden_layer = np.maximum(0,np.dot(X,w)+b) scores = np.dot(hidden_layer,w2) + b2 predicted_class = np.argmax(scores,axis = 1) print ‘training accuracy: %.2f‘ %(np.mean(predicted_class == y)) h=0.02 x_min , x_max = X[:,0].min() - 1, X[:,0].max() + 1 y_min , y_max = X[:,1].min() - 1, X[:,1].max() +1 xx, yy = np.meshgrid(np.arange(x_min , x_max ,h), np.arange(y_min , y_max ,h)) Z = np.dot(np.maximum(0,np.dot(np.c_[xx.ravel(),yy.ravel()],w)+b),w2) + b2 Z = np.argmax(Z,axis = 1) Z = Z.reshape(xx.shape) fig = plt.figure() plt.contourf(xx,yy,Z,cmap=plt.cm.Spectral,alpha=0.8) plt.scatter(X[:,0],X[:,1],c=y,s=40,cmap=plt.cm.Spectral) plt.xlim(xx.min(),xx.max()) plt.ylim(yy.min(),yy.max()) plt.show()
上述网络在迭代时,到了后期loss也没有饱和,我们将迭代期改为2000次,loss由原来的1点几降为0.3几且未饱和,accuracy达到97%.效果图如下:
注意:在编写上述代码时要注意矩阵的操作!
Deep Learning入门视频(下)之关于《感受神经网络》两节中的代码解释
标签:import sof .sh 准确率 example 开始 color div alt
原文地址:http://www.cnblogs.com/zf-blog/p/6073029.html