《机器学习实战》学习笔记——第2章 KNN

标签：相同   src   hang   对齐   ase   学习笔记   维数   枚举   另一个   

一. KNN原理：

1. 有监督的学习

根据已知事例及其类标，对新的实例按照离他最近的K的邻居中出现频率最高的类别进行分类。伪代码如下：

　　1）计算已知类别数据集中的点与当前点之间的距离

　　2）按照距离从小到大排序

　　3）选取与当前点距离最小的k个点

　　4）确定这k个点所在类别的出现频率

　　5）返回这K个点出现频率最高的类别作为当前点的预测分类

 1 import numpy as np
 2 
 3 # 读取数据
 4 def file2matrix(filename):
 5     fr = open(filename)
 6     arrayLines = fr.readlines()
 7     numbersOfArray = len(arrayLines)
 8 
 9     df = np.zeros((numbersOfArray, 3))
10     classLabel = []
11     index = 0
12 
13     for line in arrayLines:
14         # 截取掉所有的回车字符
15         line = line.strip()
16         # 使用\t将上一步得到的整行数据切分成一个元素列表
17         listFromLine = line.split(‘\t‘)
18         df[index] = listFromLine[0:3]
19         classLabel.append(listFromLine[-1])
20         index +=1
21 
22     return df, classLabel
23 filename = ‘\datingTestSet.txt‘
24 df, classLabel = file2matrix(filename)

2. KNN缺点：

（1）KNN算法是基于实例的学习，使用算法时我们必须有接近实际数据的训练样本数据。KNN必须保存全部数据集，如果训练数据集的很大，必须使用大量的存储空间。 

（2）必须对数据集中的每个数据计算距离值，耗时非常大

（3）它无法给出任何数据的基础结构信息， 因此我们无法知晓平均实例样本和典型事例样本具有什么特征

二. 使用sklearn.neighbors

1 from sklearn import neighbors
2 import numpy as np
3 
4 x = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
5 y = [1, 1]
6 nbr = neighbors.NearestNeighbors(n_neighbors=2, algorithm=‘auto‘).fit(x)
7 distance, indices = nbr.kneighbors(y)

结果：

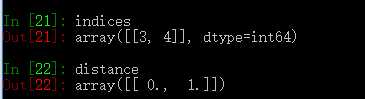
 最近邻算法主要分为三种：

（1）Brute Force

• 对于N个实例在D维中，枚举计算，时间复杂度：
• 随着N增加，时间消耗相当大

（2）K-D tree

1. 什么叫做K_Dtree：

K：K邻近查询中的k；D：空间是D维空间（Demension）tree：二叉树

2. 建树过程：

K-D tree的建立就是分裂空间的过程

• 首先我们来定义树节点的状态：

分裂点（split_point）

分裂方式（split_method）

左儿子（left_son）

右儿子（right_son）

•  建树依据：

　　先计算当前区间 [ L , R ] 中（这里的区间是点的序号区间，而不是我们实际上的坐标区间），每个点的坐标的每一维度上的方差，取方差最大的那一维，设为 d，作为我们的分裂方式（split_method ），把区间中的点按照在 d 上的大小，从小到大排序，取中间的点 sorted_mid 作为当前节点记录的分裂点，然后，再以 [ L , sorted_mid-1 ] 为左子树建树 ， 以 [sorted_mid+1 , R ] 为右子树建树，这样，当前节点的所有状态我们便确定下来了：

                split_point= sorted_mid

                split_method= d

                left_son =  [ L , sorted_mid-1 ]

                right_son =  [ sorted_mid+1 , R ]

• 举例：

　　假设现在我们有平面上的点集 E ，其中有 5 个二维平面上的点 ： （1,4）（5,8） （4,2） （7,9） （10，11）

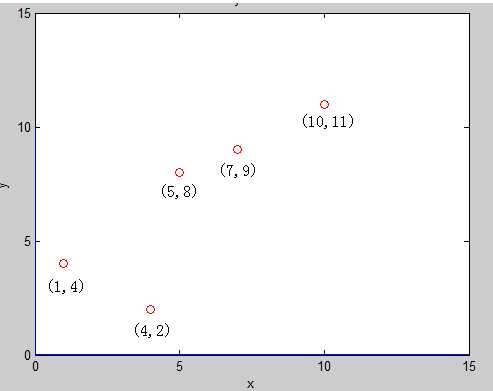
 首先，我们对整个区间 [1 , 15] 建树：先计算区间中所有点在第一维（也就是 x 坐标）上的方差：

　　平均值 ： ave_1 =5.4

　　方差 ： varance_1 =9.04

 再计算区间中所有点在第二维（也就是 y 坐标）上的方差：

　　平均值：ave_2 =6.8

　　方差：varance_2 =10.96

明显看见，varance_2 > varance_1 ，那么我们在本次建树中，分裂方式 ：split_method =2 ， 再将所有的点按照第2维的大小从小到大排序，得到了新的点的一个排列：

                （4,2） （1,4）（5,8） （7,9） （10,11）

        取中间的点作为分裂点 sorted_mid =（5，8）作为根节点，再把区间 [1 , 2] 建成左子树 , [4 , 5] 建成右子树，此时，直线 ： y = 8 将平面分裂成了两半，前面一半给左儿子，后面一半给了右儿子，如图：

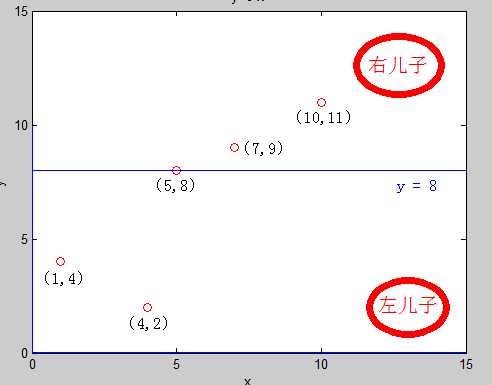
建左子树 [1, 3] 的时候可以发现，这时候第一维的方差大 ，分裂方式就是1 ，把区间 [ 1, 2 ] 中的点按照 第一维 的大小，从小到大排序 ，取中间点（1,4） 根节点，再以区间 [ 2, 2] 建立右子树 得到节点 （4,2）

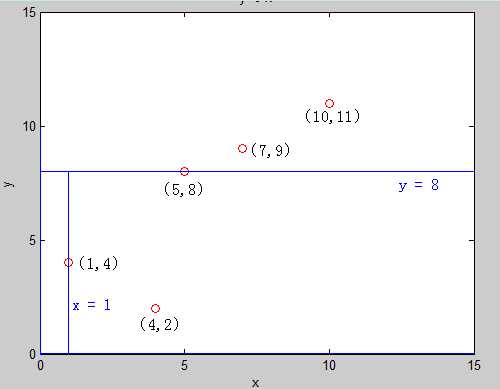
建右子树 [4 , 5] 的时候可以发现，这时还是第一维的方差大， 于是，我们便得到了这样的一颗二叉树 也就是 K-D tree，它把平面分成了如下的小平面，使得每个小平面中最多有一个点：

3. 查询过程：

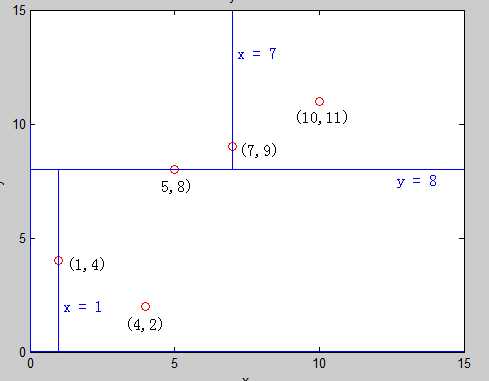
　　查询，其实相当于我们要将一个点“添加”到已经建好的 K-D tree 中，但并不是真的添加进去，只是找到他应该处于的子空间即可，所以查询就显得简单的。

　　每次在一个区间中查询的时候，先看这个区间的分裂方式是什么，也就是说，先看这个区间是按照哪一维来分裂的，这样如果这个点对应的那一维上面的值比根节点的小，就在根节点的左子树上进行查询操作，如果是大的话，就在右子树上进查询操作。

　　每次回溯到了根节点（也就是说，对他的一个子树的查找已经完成了）的时候，判断一下，以该点为圆心，目前找到的最小距离为半径，看是否和分裂区间的那一维所构成的平面相交，要是相交的话，最近点可能还在另一个子树上，所以还要再查询另一个子树，同时，还要看能否用根节点到该点的距离来更新我们的最近距离。为什么是这样的，我们可以用一幅图来说明：

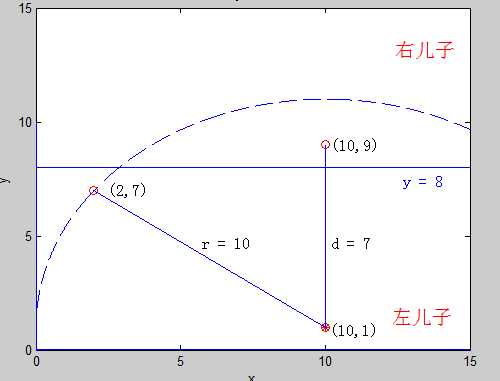
　　在查询到左儿子的时候，我们发现，现在最小的距离是 r = 10 ，当回溯到父亲节点的时候，我们发现，以目标点（10,1）为圆心，现在的最小距离 r = 10 为半径做圆，与分割平面 y = 8 相交，这时候，如果我们不在父亲节点的右儿子进行一次查找的话，就会漏掉（10,9） 这个点，实际上，这个点才是距离目标点 （10,1） 最近的点

　　由于每次查询的时候可能会把左右两边的子树都查询完，所以，查询并不是简单的 log(n) 的，最坏的时候能够达到 sqrt(n)

4. 在对样本实例进行KD-tree算法

KD（K-dimensional tree）树形结构。KD tree是二叉树

• 原理：如果我们知道A与B非常近，B与C非常近，我们就假定认为A与C非常近，不用确切的计算出他们的距离
• 计算复杂度： 
• 对参数空间沿着数据轴（N）进行划分，KDtree 很高效，因为划分过程是在参数轴（N）上进行，而不用管D实例维数
• 但是只有当D很小（D<20）的时候，运算块，当D大时，计算也会变慢
• 对于上面代码，只需修改,algorithm=‘KDTree‘

1 nbr = neighbors.NearestNeighbors(n_neighbors=2, algorithm=‘KDTree‘).fit(x)

（3）Ball tree

　　1. 原理：

　　为了改进KDtree的二叉树树形结构，并且沿着笛卡尔坐标进行划分的低效率，ball tree将在一系列嵌套的超球体上分割数据。也就是说：使用超球面而不是超矩形划分区域。虽然在构建数据结构的花费上大过于KDtree，但是在高维甚至很高维的数据上都表现的很高效。

　　球树递归地将数据划分为由质心C和半径r定义的节点，使得节点中的每个点都位于由r和C定义的超球内。通过使用三角不等式来减少邻居搜索的候选点数量的

2. 划分

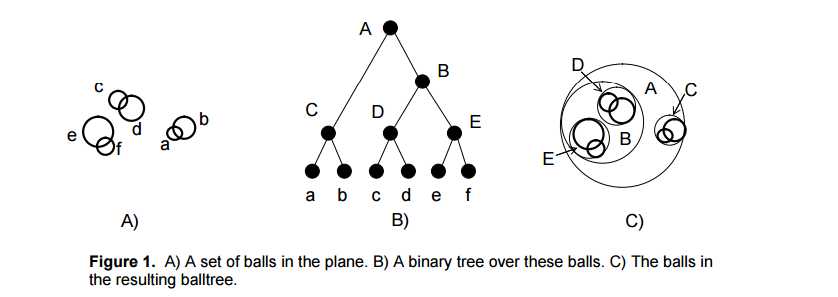
　　选择一个距离当前圆心最远的观测点i1，和距离i1最远的观测点 i2，将圆中所有离这两个点最近的观测点都赋给这两个簇的中心，然后计算每一个簇的中心点和包含所有其所属观测点的最小半径。对包含n个观测点的超圆进行分割，只需要线性的时间。　　

3. 查询

　　使用ball tree时，先自上而下找到包含target的叶子结点（c, r），从此结点中找到离它最近的观测点。这个距离就是最近邻的距离的上界。检查它的兄弟结点中是否包含比这个上界更小的观测点。方法是：如果目标点距离兄弟结点的圆心的距离 > 兄弟节点所在的圆半径 + 前面的上界的值，则这个兄弟结点不可能包含所要的观测点。否则，检查这个兄弟结点是否包含符合条件的观测点。

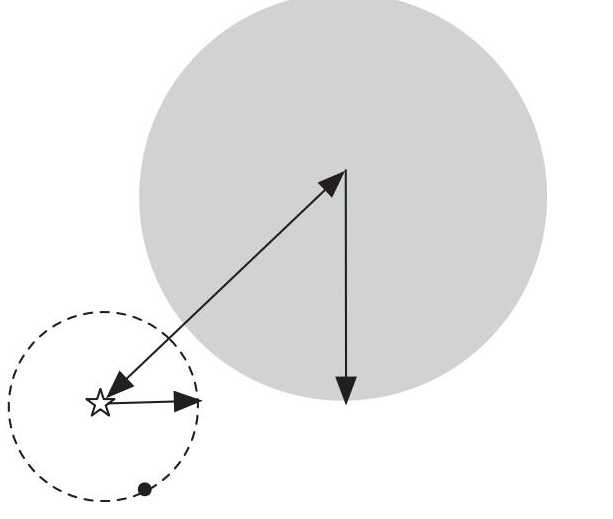
如果：该点的最近距离上确界+兄弟节点的半径 > 该点到兄弟节点圆心的距离，则表明构成了三角形，两个圆必然相交

4. 在对样本实例进行ball tree算法

• 对于上面代码，只需修改,algorithm=‘ball_tree‘

nbr = neighbors.NearestNeighbors(n_neighbors=2, algorithm=‘ball_tree‘).fit(x)

（4）选择何种算法

1. 各算法时间复杂度：N:样本数量，D:特征向量

• Brute force query time grows as 
• Ball tree query time grows as approximately 
• KD tree query time changes with  in a way that is difficult to precisely characterise. For small  (less than 20 or so) the cost is approximately , and the KD tree query can be very efficient. For larger , the cost increases to nearly , and the overhead due to the tree structure can lead to queries which are slower than brute force.

对于小数据集（N小于30左右）， log（N）可以与N比较，并且强力算法可以比基于树的方法更有效。KDTree和BallTree都通过提供叶大小参数来解决这个问题：这控制了查询切换到暴力的样本数。 这允许两个算法接近小于N的强力计算的效率。

2. 数据结构：

数据的内在维度或数据的稀疏性。 内在维度是指数据所在的D，其可以线性地或非线性地嵌入参数空间中。 稀疏性指的是数据填充参数空间的程度（这与“稀疏”矩阵中使用的概念区分开来。数据矩阵可以没有零项，但是结构在这个项中仍然可以是“稀疏的” ）。

• 强制查询时间根据数据结构不变。
• ball tree和KD树查询时间会受到数据结构的很大影响。 一般来说，具有较小固有维度的稀疏数据导致更快的查询时间。 由于KD树内部表示与参数轴对齐，因此对于任意结构化数据，它通常不会显示与ball tree相同的改进。

机器学习中使用的数据集往往是非常结构化的，非常适合基于树的查询。

3. 可以自动选择：

nbr = neighbors.NearestNeighbors(n_neighbors=2, algorithm=‘auto‘).fit(x)

目前，如果k <N / 2并且‘effective_metric_‘在‘kd_tree‘的‘VALID_METRICS‘列表中，algorithm =‘auto‘选择‘kd_tree‘。 如果k <N / 2并且‘effective_metric_‘不在‘kd_tree‘的‘VALID_METRICS‘列表中，它选择‘ball_tree‘。 如果k> = N / 2，则选择“brute”。 该选择基于如下假设：查询点的数量至少与训练点的数量相同，并且该leaf_size接近其默认值30。

《机器学习实战》学习笔记——第2章 KNN

标签：相同   src   hang   对齐   ase   学习笔记   维数   枚举   另一个   

原文地址：http://www.cnblogs.com/lesleysbw/p/6074662.html