标签:head png 提高 整数 algorithm 依次 最大 style 连通图
无向连通图G 有n 个点,n - 1 条边。点从1 到n 依次编号,编号为 i 的点的权值为W i ,每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ,若它们的距离为2 ,则它们之间会产生Wu
×Wv 的联合权值。
请问图G 上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
输入格式:
输入文件名为link .in。
第一行包含1 个整数n 。
接下来n - 1 行,每行包含 2 个用空格隔开的正整数u 、v ,表示编号为 u 和编号为v 的点之间有边相连。
最后1 行,包含 n 个正整数,每两个正整数之间用一个空格隔开,其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。
输出格式:
输出文件名为link .out 。
输出共1 行,包含2 个整数,之间用一个空格隔开,依次为图G 上联合权值的最大值
和所有联合权值之和。由于所有联合权值之和可能很大,[b]输出它时要对10007 取余。 [/b]
5 1 2 2 3 3 4 4 5 1 5 2 3 10
20 74
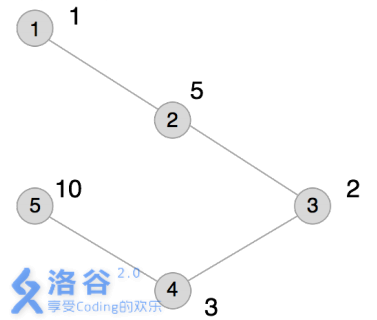
本例输入的图如上所示,距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。
其联合权值分别为2 、15、2 、20、15、20。其中最大的是20,总和为74。
【数据说明】
对于30% 的数据,1 < n≤ 100 ;
对于60% 的数据,1 < n≤ 2000;
对于100%的数据,1 < n≤ 200 , 000 ,0 < wi≤ 10, 000 。
选定一个点,找寻与它距离为2的点←无疑太过复杂。
转换思路,选定一个点,找出所有与它相连的点,这些点两两距离都为2
这样问题就简单多了。
依次处理每一个点u,将该点连接的所有点v的权值累加起来,记为s1,点v在统计点u时贡献的权值为(s1-w[v])*w[v] ←乘法原理。
求最大联合权值的思路类似,详见代码。
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 using namespace std; 6 struct Edge{ 7 int next; 8 int to; 9 int w; 10 }edge[600500]; 11 int head[500000],u,v,ct=0; 12 int w[300100]; 13 long long sum; 14 long long mxsum; 15 void add_edge(int fr,int t){ 16 edge[++ct].next=head[fr]; 17 edge[ct].to=t; 18 head[fr]=ct; 19 return; 20 } 21 int sch(int st){//st-第st个点 22 int i,j; 23 int num=0; 24 int c[150100]; 25 long long s1=0; 26 int m1=0,m2=0; 27 for(j=head[st];j;j=edge[j].next){ 28 num++; 29 c[num]=w[edge[j].to]; 30 s1+=c[num]; 31 } 32 for(i=1;i<=num;i++){ 33 sum=(sum+(s1-c[i])*c[i])%10007; 34 35 if(c[i]>m1){ 36 m2=m1;m1=c[i]; 37 } 38 else if(c[i]>m2)m2=c[i]; 39 // printf("%d: %d %d\n",st,m1,m2); 40 } 41 if(num)if(m1*m2>mxsum)mxsum=m1*m2; 42 43 if(sum<0)sum+=10007; 44 return 0; 45 } 46 47 int main(){ 48 int i,j; 49 int n; 50 scanf("%d",&n); 51 for(i=1;i<n;i++){ 52 scanf("%d%d",&u,&v); 53 add_edge(u,v); 54 add_edge(v,u); 55 } 56 for(i=1;i<=n;i++)scanf("%d",&w[i]); 57 for(i=1;i<=n;i++){ 58 sch(i); 59 } 60 cout<<mxsum<<" "<<sum; 61 return 0; 62 }
标签:head png 提高 整数 algorithm 依次 最大 style 连通图
原文地址:http://www.cnblogs.com/SilverNebula/p/6078672.html