POJ 1692 Crossed Matchings(DP)

标签：acm   poj   动态规划   dp   

题意  有两行数a[n1] b[n2]   分别有n1 n2个数   当第一行一个数和第二行一个数相等时   他们就可以连起来   每个数只能连一个   求最有多少条线使得每条都至少有一条和它相交

令d[i][j]表示  a的前i个数和j的前j个数最多可以连接多少条

当a[i]==b[j]时  将们连起来是肯定不与其它线相交的  所以d[i][j]=max(d[i-1][j],d[i][j-1])

当a[i]!=b[j]时   如果可以在第一行找一个数x<i  第二行找一个数y<j  使得a[x]==b[j]  b[y]==a[i]  那么有d[i][j]=max(d[x][y]+2,d[i-1][j],d[i][j-1])   如果找不到d[i][j]=max(d[i-1][j],d[i][j-1])

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 105;
int a[N], b[N], d[N][N], la, lb, cas;
int main()
{
    scanf ("%d", &cas);
    while (cas--)
    {
        scanf ("%d%d", &la, &lb);
        for (int i = 1; i <= la; ++i)
            scanf ("%d", &a[i]);
        for (int j = 1; j <= lb; ++j)
            scanf ("%d", &b[j]);

        for (int i = 1; i <= la; ++i)
            for (int j = 1; j <= lb; ++j)
            {
                d[i][j] = max (d[i][j - 1], d[i - 1][j]);
                int x, y;
                for (x = i - 1; x >= 1; --x)
                    if (a[x] == b[j]) break;
                for (y = j - 1; y >= 1; --y)
                    if (a[i] == b[y]) break;

                if (x && y && a[i] != b[j])
                    d[i][j] = max (d[x - 1][y - 1] + 2, d[i][j]);
            }

        printf ("%d\n", d[la][lb]);
    }
    return 0;
}

Description

There are two rows of positive integer numbers. We can draw one line segment between any two equal numbers, with values r, if one of them is located in the first row and the other one is located in the second row. We call this line segment an r-matching segment. The following figure shows a 3-matching and a 2-matching segment. 

We want to find the maximum number of matching segments possible to draw for the given input, such that: 
1. Each a-matching segment should cross exactly one b-matching segment, where a != b . 
2. No two matching segments can be drawn from a number. For example, the following matchings are not allowed. 

Write a program to compute the maximum number of matching segments for the input data. Note that this number is always even.

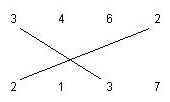
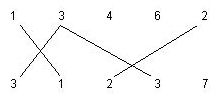
Input

Output

Sample Input

3
6 6
1 3 1 3 1 3
3 1 3 1 3 1
4 4
1 1 3 3 
1 1 3 3 
12 11
1 2 3 3 2 4 1 5 1 3 5 10
3 1 2 3 2 4 12 1 5 5 3 

Sample Output

6
0
8

POJ 1692 Crossed Matchings(DP),布布扣,bubuko.com

POJ 1692 Crossed Matchings(DP)

标签：acm   poj   动态规划   dp   

原文地址：http://blog.csdn.net/iooden/article/details/38584625