标签:code 正整数 else stdio.h 自定义函数 函数实现 gcd 输出 case
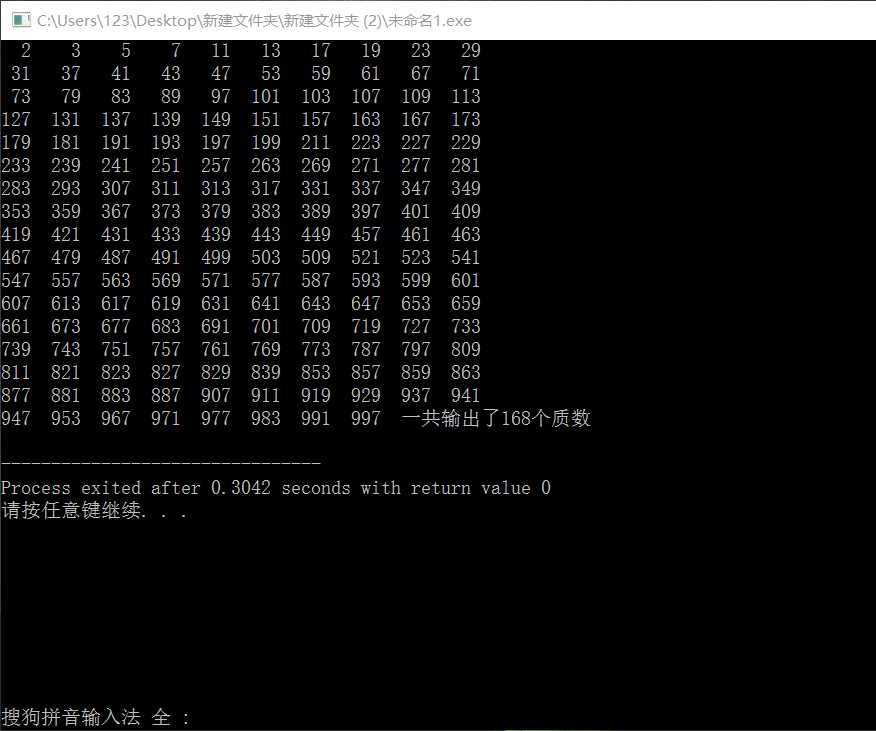
1. 定义一个判断素数的函数isprime(int n),利用该函数输出1000以内的所有素数,每行10个,最后输出一共有多少个素数。(每列对齐)
#include <stdio.h> int isprime(int a); int main() { int a,b=0; for(a=2;a<=1000;a++) { if(isprime(a)) { printf("%3d ",a); b++; if(b%10==0) { printf("\n"); } } } printf("一共输出了%d个质数\n",b); } int isprime(int a) { int i; for(i=2;i<=a-1;i++) { if(a%i==0) { return 0; } } return 1; }
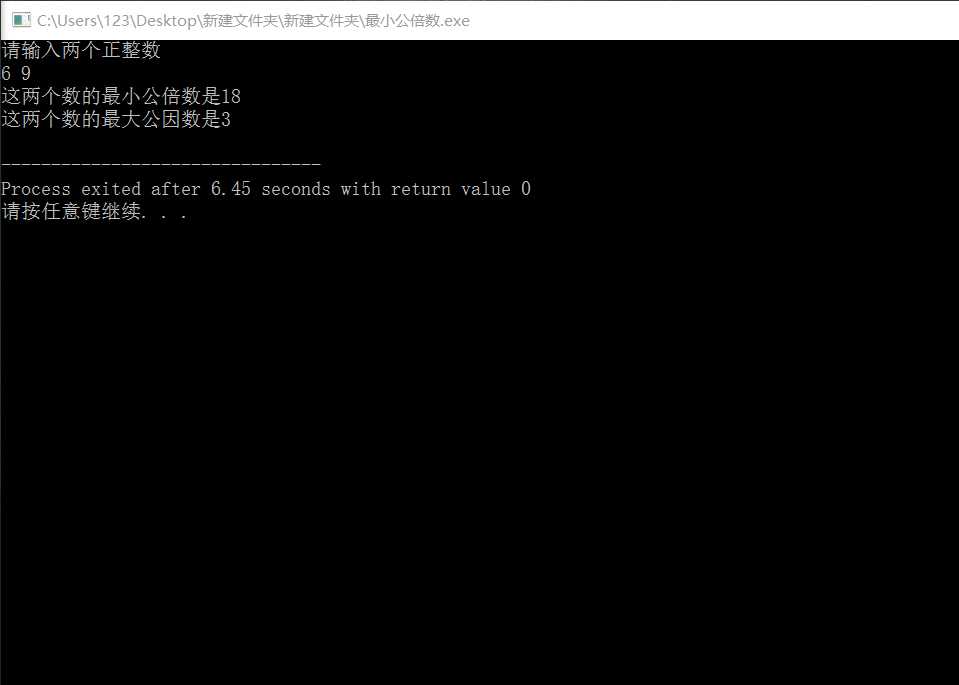
2.求两个正整数的最大公约数和最小公倍数。用一个函数gcd(int a,int b)求最大公约数,另一个函数lcm(int a,int b)根据求出的最大公约数求最小公倍数。
#include<stdio.h> int gcd(int a,int b); int lcm(int a,int b); int main() { int a,b; printf("请输入两个正整数\n"); scanf("%d%d",&a,&b); printf("这两个数的最小公倍数是%d\n",lcm(a,b)); printf("这两个数的最大公因数是%d\n",gcd(a,b)); return 0; } int gcd(int a,int b) { int s; if(a<b) { s=a; a=b; b=s; } while(b!=0) { s=a%b; a=b; b=s; } return a; } int lcm(int a,int b) { int m; m=a*b/gcd(a,b); }
3:不会。
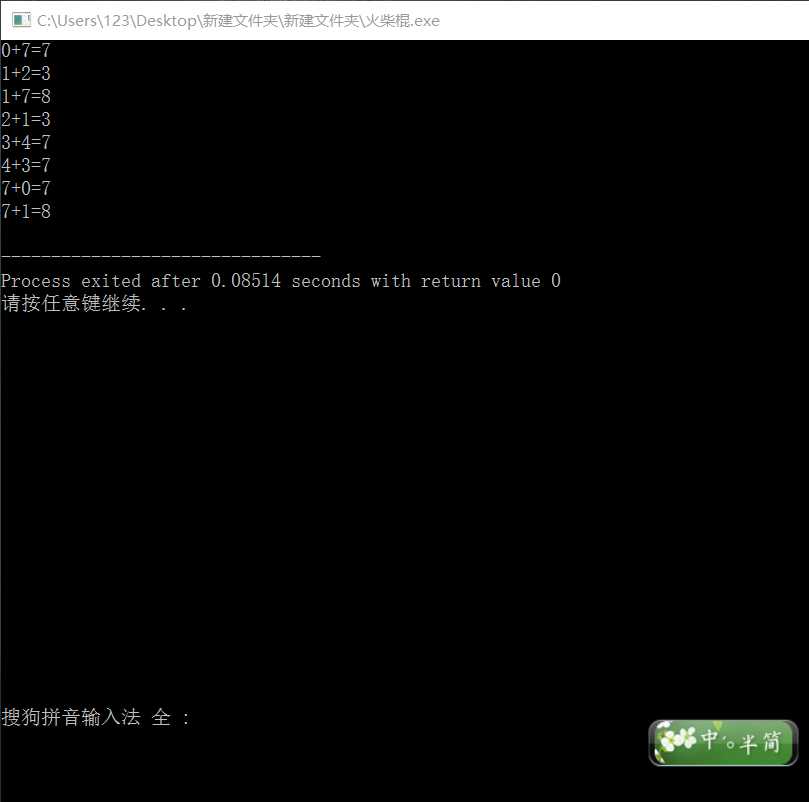
4.用函数实现:火柴棍等式问题。
# include<stdio.h> int gen(int m); int main() { int a,b,c,d,e,f; for(a=0;a<=9;a++) for(b=0;b<=9;b++) { c=a+b; if(c>9) { break; } else { d=gen(a); e=gen(b); f=gen(c); if(d+e+f==12) { printf("%d+%d=%d\n",a,b,c); } } } return 0; } int gen(int m) { int n; switch(m) { case 0: case 6: case 9:n=6;break; case 1:n=2;break; case 2: case 3: case 5:n=5;break; case 4:n=4;break; case 7:n=3;break; case 8:n=7;break; } return n; }
实验总结:
1:程序中有输出三位数所以要弄三个字节 要不对不齐。
2:两个自定义函数可以嵌套,
4:if函数看着不整洁,必要时可以使用switch case 语句代替。
知识点总结:
1:最小公倍数是用这倆数相乘再除以最大公因数。
2:自定义函数如果有两个要(int a,int b),如果有一个就写(a);自定义函数是可以嵌套的。
4:switch 等函数的使用可以嵌套在自定义函数z中。
标签:code 正整数 else stdio.h 自定义函数 函数实现 gcd 输出 case
原文地址:http://www.cnblogs.com/endeavor992/p/6083026.html