进制转换与原码补码

标签：小数点   定位   速度   img   ges   过程   素数   取反   原因   

进制

进制也就是进位制，是人们规定的一种进位方法。

数码、位权

数码: 指集合论中刻画任意集合所含元素数量多少的一个概念

十进制的基本符号是：0、1、2、3、4、5、6、7、8、9；我们把这些称为十进制的数码：也就是基本符号，所有的十进制都是有这十个数码组成的。每位在加时都是“逢十进一”。

位权: 数制中每一固定位置对应的单位值称为位权

那么大家考虑一个问题，说一个十进制数，已知第四位是5，其它位都是0，那么这个数是几?答案：5000，怎么算的是5*10^4-1；那么就引入了一个权的概念。

对于十进制，我们可以从0开始，对数字的各个数位进行编号，即个位起从右往左依次为编号0，1，2，……；对称的，从小数点后的数位则是-1，-2，……；而n位所代表的权的大小就是10n-1;

在计算机系统中，数据以二进制信息单元0,1的形式表示。那么在计算机系统中，二进制又是怎么一回事呢？

二进制 

二进制：同十进制一样，也是计数的一种方法。

(1) 计算机中采用二进制主要原因:

1) 技术实现简单，计算机是由逻辑电路组成，逻辑电路通常只有两个状态，开关的接通与断开，这两种状态正好可以用“1”和“0”表示。

2) 简化运算规则:两个二进制数和、积运算组合各有三种，运算规则简单，有利于简化计算机内部结构，提高运算速度。

3) 适合逻辑运算:逻辑代数是逻辑运算的理论依据，二进制只有两个数码，正好与逻辑代数中的“真”和“假”相吻合。

4) 易于进行转换，二进制与十进制数易于互相转换。

5) 用二进制表示数据具有抗干扰能力强，可靠性高等优点。因为每位数据只有高低两个状态，当受到一定程度的干扰时，仍能可靠地分辨出它是高还是低

(2) 二进制的数码：0和1，“逢二进一”。

(3) 二进制数的表示形式：方法一：（100001）₂     方法二：100001B

(4) 二进制的权位：n位上的数值代表是2^n-1,如二进制数100001到底是我们生活当中十进制的几呢？

(5) 二进制转换十进制：方法是按权位求和

二进制数100001=1*2^6-1+0*2^5-1+0*2^4-1+0*2^3-1+0*2^2-1+1*2^1-1=32+1=33（注：中间计算过程都是十进制）

(6) 二进制同十进制一样也可以进行加减乘除算术四则运算，还可以进行逻辑运算。下面我们就来看一下二进制的运算。

(7) 二进制的四则运算：

1000011+111001=？（和十进制加法一样只是逢二进一即可）

1000011-111001=？（和十进制减法一样只是不够减，向前一位借，每次借2）

二进制的乘法和除法和十进制也是一样的，这里就不做过多的表述了。

那么十进制又是如何转换成二进制呢？这里只讨论能转换成的整数，不讨论小数。

我们以100转换成二进制为例来说：方法是用除二取余法，在讲这个方法之前，我们先来看一个式子，在小学三年级的时候就学过，9÷2=4----1，2我们称为商（取整），1我们称为余（余数）。

除二取余法：依次除二求余直至最后为0，然后从下向上依次写下每次的余数组成新数。

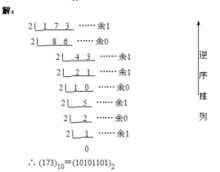
这种方法，可以把十进制数转换成任意n进制的数，除n取余法。

学习完十进制，二进制，不得不说下八进制和十六进制，因为二进制表示一个大数时位数太多，所以又提出了八进制、十六进制的概念。

八进制数

由于二进制数据的基R较小，所以二进制数据的书写和阅读不方便，为此，在小型机中引入了八进制。八进制的基R=8=2^3，有数码0、1、2、3、4、5、6、7，并且每个数码正好对应三位二进制数，所以八进制能很好地反映二进制。八进制用下标8或数据后面加O表示 例如：二进制数据 （ 11 101 010 . 010 110 100 ）2 对应 八进制数据 ( 3 5 2 . 2 6 4 )8或352.264O.

十六进制

由于二进制数在使用中位数太长，不容易记忆，所以又提出了十六进制数

十六进制数有两个基本特点：它由十六个字符0～9以及A，B，C，D，E，F组成（它们分别表示十进制数10～15），十六进制数运算规律是逢十六进一，即基R=16=2^4，通常在表示时用尾部标志H或下标16以示区别。

例如：十六进制数4AC8可写成（4AC8）16，或写成4AC8H。

二进制数与十六进制数之间的转换

由于4位二进制数恰好有16个组合状态，即1位十六进制数与4位二进制数是一一对应的.所以，十六进制数与二进制数的转换是十分简单的.

(1) 十六进制数转换成二进制数，只要将每一位十六进制数用对应的4位二进制数替代即可――简称四位一分.

例：将（4AF8B)16转换为二进制数.

解： 4 A F 8 B

0100 1010 1111 1000 1011

所以（4AF8B)16=(1001010111110001011)₂

(2) 二进制数转换为十六进制数，分别向左，向右每四位一组，依次写出每组4位二进制数所对应的十六进制数――简称四位合一位.

例：将二进制数（000111010110)₂转换为十六进制数.

解： 0001 1101 0110

1 D 6

所以（111010110)2=（1D6）16

转换时注意最后一组不足4位时必须加0补齐4位

(3) 二进制与八进制互转和二进制转十六进制相似只是每三位二进制转成一位八进制，而一位八进制数转换成三位二进制数。

(4) 知道数制之间的转换也就理解了数值之间怎么进行运算的，那我们在计算机中到底是怎么把输入电脑的100+100进行运算的呢？那么就要理解原码、反码及补码。

机器数

一个数在计算机中的二进制表示形式,  叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为0, 负数为1.

比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。

那么，这里的 00000011 和 10000011 就是机器数。

真值

因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是-3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。

例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1

原码、反码及补码：

首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.

于是人们为了将符号位参与运算, 并且只保留加法，从而简化计算机运算，发明了原码、反码和补码。

原码, 反码, 补码都是有符号的用二进制表示数的方法.均由符号位和数值位构成 

原码

原码是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

[+1]原 = 0000 0001

[-1]原 = 1000 0001

第一位是符号位.余下7位是数值位。 因为第一位是符号位, 所以8位二进制数的取值范围就是:

[1111 1111 , 0111 1111]

即

[-127 , 127]

原码是人脑最容易理解和计算的表示方式.

反码

反码的表示方法是:

正数的反码是其本身

负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.

[+1] = [00000001]原 = [00000001]反

[-1] = [10000001]原 = [11111110]反

可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.

补码

补码的表示方法是:

正数的补码就是其本身

负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

[+1] = [00000001]原 = [00000001]反 = [00000001]补

[-1] = [10000001]原 = [11111110]反 = [11111111]补

对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.

在计算机系统中，数值一律用补码来表示（存储）。 主要原因：使用补码，可以将符号位和其它位统一处理；同时，减法也可按加法来处理。另外，两个用补 码表示的数相加时，如果最高位（符号位）有进位，则进位被舍弃；补码与原码的转换过程几乎是相同的。

进制转换与原码补码

标签：小数点   定位   速度   img   ges   过程   素数   取反   原因   

原文地址：http://www.cnblogs.com/lcgsmile/p/6085213.html