标签:相加 bsp images 调整 等于 所有结点 插入 .com 解释
1、什么是B树(B-树)?
B树是一种m阶树,m>=2
性质:
1)树中每个结点至多m个孩子;
2)对于根结点,子树个树取值范围为[2,m],关键字个数范围[1,m-1];
3)对于非根非叶结点,子树个数取值范围为[ceil(m/2),m],关键字个数范围为[ceil(m/2)-1,m-1];
4)所有叶子结点都出现在同一层。
5)每个非叶子结点中包含n个关键字信息:(n, P0, K1, P1, K2, P2, ... , Kn, Pn)。
n为关键字的个数,且有 [ceil(m/2)-1] <= n <= m-1
Ki为关键字,且按升序排序
Pi为指向子树的接点,且 K(i-1) <= P(i-1) 指向子树的所有结点关键字 <=Ki
三阶B树
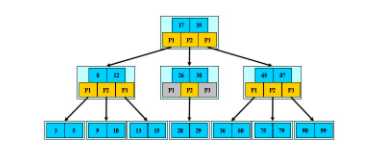
2)3)的应用
如果B树结点的最小度数为固定整数t>=2,有
a) 非根结点至少 t-1个关键字,非根非叶结点至少t个子女
b)每个结点至多2t-1个关键字,每个非根非叶结点至多2t个子女
c)综上所述根结点关键字个数范围为:[1, 2*t-1],非根结点关键字个数范围为:[t-1,2*t-1]
2、B树复杂度与高度
B树的高度:
根为1个结点,第二层至少为2个结点,第三层至少为2t个结点,第四层至少2t*t个结点
将所有最小结点相加,推导过程:n>= 1+2+2t+2t^2+ ... +2t^(h-1)=3+2t (t^h-1)/(t-1)>=2t^(h-1)+1
最后推出的结果为
h<=log((n-1)/2)
3、操作
这里只给出插入删除操作,查找操作相对简单的多 这里不做解释
1)B-树的插入操作(重点判断是否满足n<=m-1)
a.利用前述的B-树的查找算法查找关键字的插入位置。若找到,则说明该关键字已经存在,直接返回。否则查找操作必失败于某个最低层的非终端结点上。
b.判断该结点是否还有空位置。即判断该结点的关键字总数是否满足n<=m-1。若满足,则说明该结点还有空位置,直接把关键字k插入到该结点的合适位置上。若不满足,说明该结点己没有空位置,需要把结点分裂成两个。
分裂的方法是:生成一新结点。把原结点上的关键字和k按升序排序后,从中间位置把关键字(不包括中间位置的关键字)分成两部分。左部分所含关键字放在旧结点中,右部分所含关键字放在新结点中,中间位置的关键字连同新结点的存储位置插入到父结点中。如果父结点的关键字个数也超过(m-1),则要再分裂,再往上插。直至这个过程传到根结点为止。
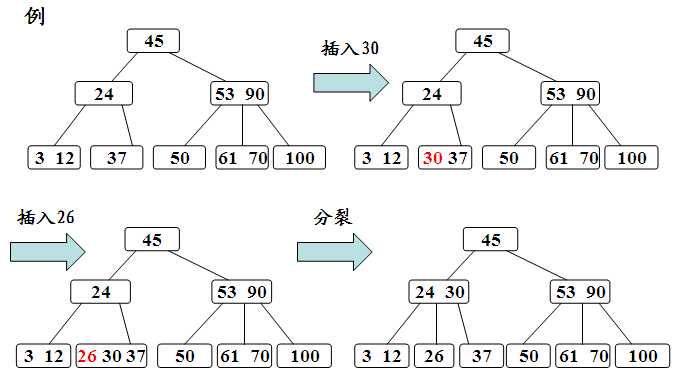
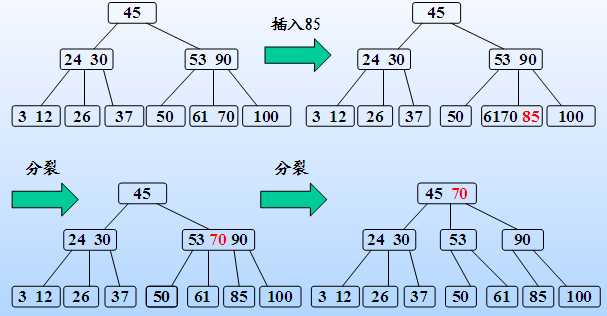
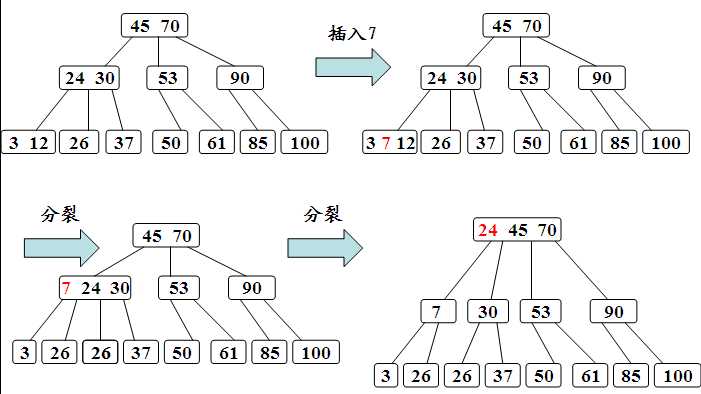
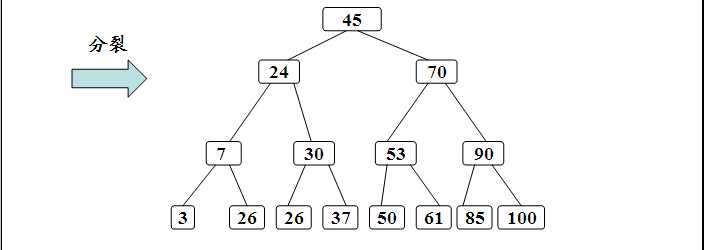
2)B树的删除
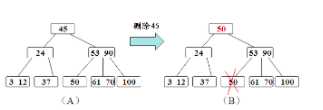
a)利用B树查找算法找出关键字所在的结点,然后根据结点所在的位置判断是否为叶子结点
b)若为非叶结点,且被删关键字为该结点中第i个关键字key[i],则可从指针son[i]所指向的子树中找出最小关键字Y,代替key[i]的位置,然后在叶结点中删去Y,把非叶结点的删除化为叶结点的删除。
叶结点删除一个关键字的方法:
三种不同情况:
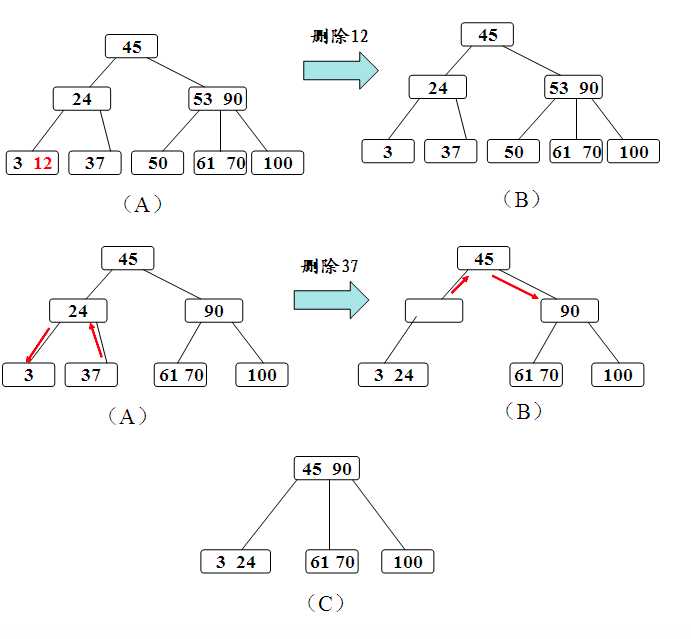
(1)如果被删关键字所在结点的原关键字个数n>ceil(m/2),则说明删去该关键字后该结点仍满足B树的定义,这种情况下直接删除即可;
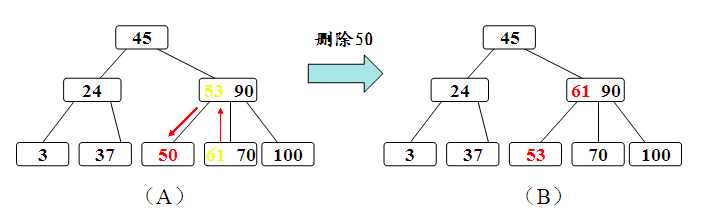
(2)如果被删除关键字所在结点的关键字个数n等于ceil(m/2)-1,说明删去该关键字后该结点将不满足B树的定义,需要调整:
如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的左(右)兄弟结点中的关键字数目大于ceil(m/2)-1,则可将左(右)兄弟结点中最大(小)的结点上移至双亲结点,而将双亲结点中大(小)于该上移关键字的关键字下移至被删关键字所在结点中。
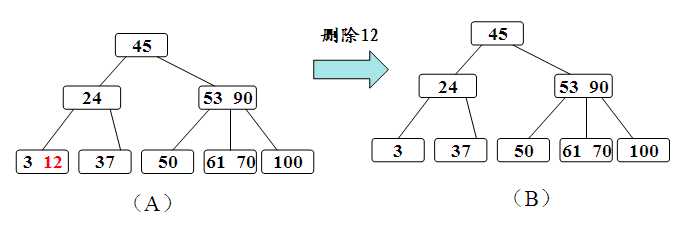
(3)如果左右兄弟结点中没有多余的关键字,即左右兄弟结点中关键字的数目均等于ceil(m/2)-1。
需要调整:
在删除关键字后,该结点中剩余的关键字加指针,加上双亲结点中的关键字(该关键字为结点与兄弟结点的分割者),合并到兄弟结点中去。
标签:相加 bsp images 调整 等于 所有结点 插入 .com 解释
原文地址:http://www.cnblogs.com/KennyRom/p/6087483.html