标签:each 降幂 pre amp src indent testcases div should
Description
Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000).
Input
Output
Sample Input
3 2 4 2 10 1000
Sample Output
1 24
Hint
Source
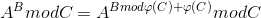
降幂公式 phi() 为欧拉函数
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #define ll __int64 5 #define mod 10000000007 6 using namespace std; 7 char a[1000006]; 8 ll x,z; 9 ll quickpow(ll x,ll y,ll z) 10 { 11 ll ans=1; 12 while(y) 13 { 14 if(y&1) 15 ans=ans*x%z; 16 x=x*x%z; 17 y>>=1; 18 } 19 return ans; 20 } 21 ll phi(ll n) 22 { 23 ll i,rea=n; 24 for(i=2;i*i<=n;i++) 25 { 26 if(n%i==0) 27 { 28 rea=rea-rea/i; 29 while(n%i==0) 30 n/=i; 31 } 32 } 33 if(n>1) 34 rea=rea-rea/n; 35 return rea; 36 } 37 int main() 38 { 39 while(scanf("%I64d %s %I64d",&x,a,&z)!=EOF) 40 { 41 ll len=strlen(a); 42 ll p=phi(z); 43 ll ans=0; 44 for(ll i=0;i<len;i++) 45 ans=(ans*10+a[i]-‘0‘)%p; 46 ans+=p; 47 printf("%I64d\n",quickpow(x,ans,z)); 48 } 49 return 0; 50 }
标签:each 降幂 pre amp src indent testcases div should
原文地址:http://www.cnblogs.com/hsd-/p/6091289.html