标签:连通 复杂 有向图 style tail 并且 分享 net com
根据我做过的一些错题。我想要简要总结一下一些比较容易忽略的图的概念。
1完全有向图和完全无向图。
一个有向图,有n个结点,则最多有n(n-1)条边。这种有n(n-1)条边的有向图是完全有向图。
一个无向图有n个节点,则最多有n(n-1)/2条边。这种n(n-1)/2条边的无向图是完全无向图。
2连通,连通图,连通分量。
在无向图中,vi到vj有路径,则说vi到vj连通。
若无向图的任意两个节点都连通,说这是连通图。
连通分量,在理解它之前,先要理解什么事极大连通子图。 A B是连通子图 A C也是连通子图
A B C也是连通子图。但是A B, A C,节点数分别是2,2少于A B C(扩充进C)连通子图的3。所以A B C是极大连通子图。
D E也是连通子图。并且没办法再扩充了。它也是极大连通子图。连通分量就是极大连通子图
所以连通分量是A B C。D E。
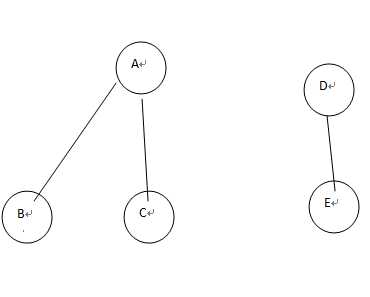
PS:一个N节点图至少一个连通分量。至多N个连通分量。
1 有环无环,深度优先搜索和拓扑排序关系。
这个问题比较复杂,第一是要知道回路。
回路 就是出发点与终点都是同一个点的路径 比如A-B-C-A。有回路就是有环的意思。
第二是要知道深度优先搜索 不要用递归实现,当数据一多就炸了。要用栈来实现,那么如何用栈实现呢?
http://blog.csdn.net/ivan_zgj/article/details/51541447这里有说。
然后用栈实现的深度优先搜索 逆序就是 拓扑排序。
标签:连通 复杂 有向图 style tail 并且 分享 net com
原文地址:http://www.cnblogs.com/zzzPark/p/6106207.html