Tensorflow学习笔记（一）：MNIST机器学习入门

标签：ace   lap   nload   回归   sdn   correct   浮点   文件   image   

     学习深度学习，首先从深度学习的入门MNIST入手。通过这个例子，了解Tensorflow的工作流程和机器学习的基本概念。

一  MNIST数据集

     MNIST是入门级的计算机视觉数据集，包含了各种手写数字的图片。在这个例子中就是通过机器学习训练一个模型，以识别图片中的数字。

     MNIST数据集来自 http://yann.lecun.com/exdb/mnist/

     Tensorflow提供了一份python代码用于自动下载安装数据集。Tensorflow官方文档中的url打不开，在CSDN上找到了一个分享：http://download.csdn.net/detail/u010417185/9588647

     和官方有点不同的是，我直接把四个数据集下载下来，放在/tmp/mnist下，在项目文件中使用以下代码导入：

import input_data
import tensorflow as tf

mnist = input_data.read_data_sets("/tmp/mnist", one_hot=True)

     这里的数据集分为两个部分：60000的训练数据集（mnist.train）和10000的测试数据集（mnist.test），测试集的作用是帮助模型泛化。数据对应包含图片和标签，分别用mnist.train.images，mnist.train.lables，mnist.test.images，mnist.test.lables来表示。每张图片有28×28=784个像素点，因此训练图片mnist.train.images的张量表示为 [60000, 784]，第一个纬度用于索引图片，第二纬度用于索引像素点。由于判断10个数字，这里采用热独，即one-hot-vectors，除了一位数字为1外其他纬度数字为0。例如判断数字为0则其表示为[1，0，0，0，0，0，0，0，0，0]。因此训练标签表示为[10000，10]，第一纬度索引图片，第二纬度判断数字。

二  softmax回归介绍

   softmax模型可以给不同的对象分配概率。根据下图，对输入的x的加权求和，再分别加上一个偏置量，最后输入到softmax函数中：

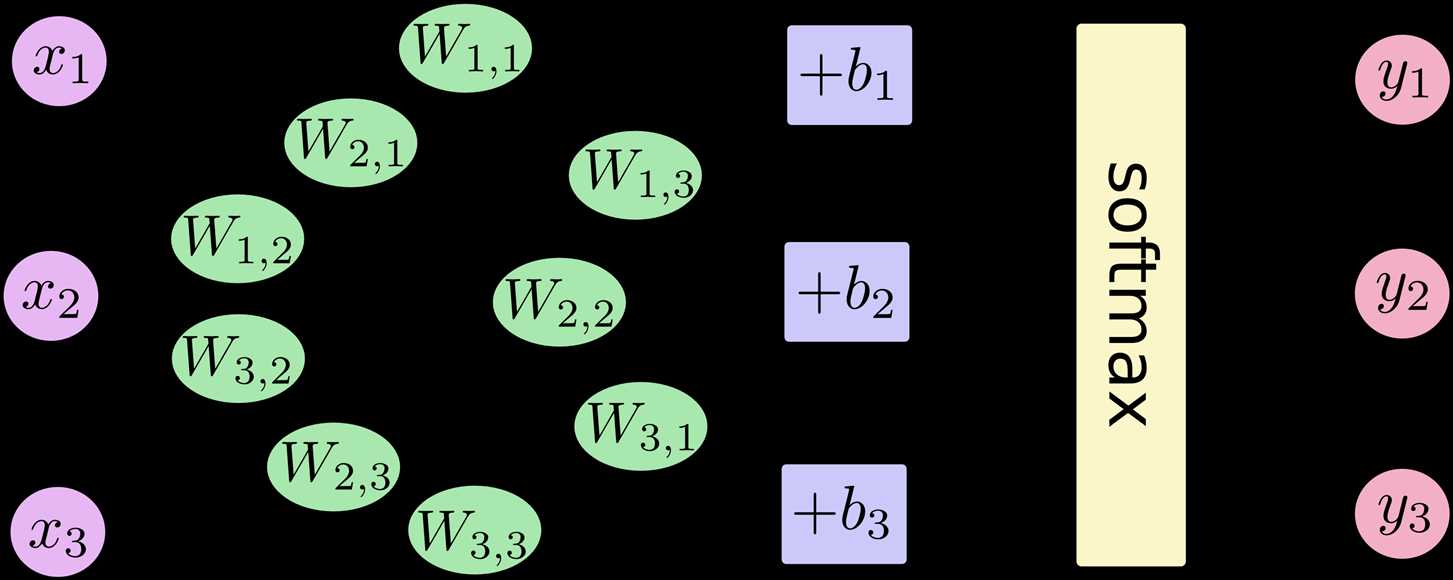
      具体转换为公式，即：

三  实现回归模型

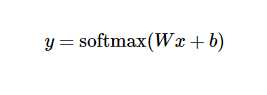
      首先进行模型的定义，如下：

x = tf.placeholder(tf.float32, [None, 784]) #使用占位符placeholder，第一维度可指定图片的数量是任意的
W = tf.Variable(tf.zeros([784,10]))  #初始化权值
b = tf.Variable(tf.zeros([10]))      #初始化偏置值
y = tf.nn.softmax(tf.matmul(x,W) + b)  #根据公式计算

四  训练模型

     选用的损失函数为交叉熵，其定义如下：

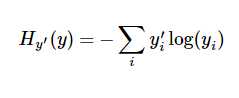
    其中y为预测的概率分布，y‘为实际分布。

    代码如下：

y_ = tf.placeholder("float", [None,10])  #表示实际的分布
cross_entropy = -tf.reduce_sum(y_*tf.log(y))  #计算损失函数
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)  #以梯度下降算法最小化损失函数
init = tf.initialize_all_variables()  #初始化所有变量
sess = tf.Session()  #定义会话
sess.run(init)   #初始化会话

for i in range(1000):   #开始训练，循环训练1000次
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

五  评估模型

    选用tf.argmax函数评估，它能给出某个tensor对象在某一维上的其数据最大值所在的索引值。由于标签向量是由0,1组成，因此最大值1所在的索引位置就是类别标签，比如tf.argmax(y,1)返回的是模型对于任一输入x预测到的标签值，而 tf.argmax(y_,1) 代表正确的标签，用 tf.equal 来检测预测是否与真实标签匹配(索引位置一样表示匹配)。

    代码如下：

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))  #评估
accuracy = tf.reduce_mean(tf.cast(correct_prediction,"float"))  #将结果转换为浮点数
print sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels})  #输出

六  代码

import input_data
import tensorflow as tf

mnist = input_data.read_data_sets("/tmp/mnist", one_hot=True)

x = tf.placeholder(tf.float32, [None, 784]) #使用占位符placeholder，第一维度可指定图片的数量是任意的
W = tf.Variable(tf.zeros([784,10]))  #初始化权值
b = tf.Variable(tf.zeros([10]))      #初始化偏置值
y = tf.nn.softmax(tf.matmul(x,W) + b)  #根据公式计算
y_ = tf.placeholder("float", [None,10])  #表示实际的分布
cross_entropy = -tf.reduce_sum(y_*tf.log(y))  #计算损失函数
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)  #以梯度下降算法最小化损失函数
init = tf.initialize_all_variables()  #初始化所有变量
sess = tf.Session()  #定义会话
sess.run(init)   #初始化会话

for i in range(1000):   #开始训练，循环训练1000次
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))  #评估
accuracy = tf.reduce_mean(tf.cast(correct_prediction,"float"))  #将结果转换为浮点数
print sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels})  #输出

View Code

七  实验结果

    最终测试结果精确度在91%左右。

Tensorflow学习笔记（一）：MNIST机器学习入门

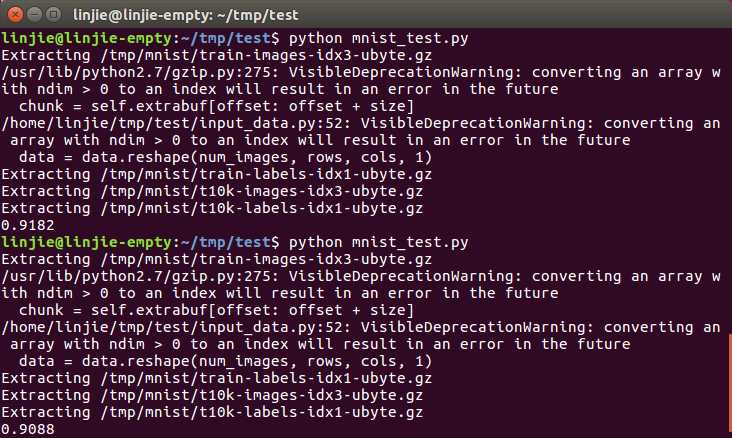
标签：ace   lap   nload   回归   sdn   correct   浮点   文件   image   

原文地址：http://www.cnblogs.com/LJ-LJ/p/6107071.html