标签:alt result 对比 测试数据 变化 range layer png 1.0
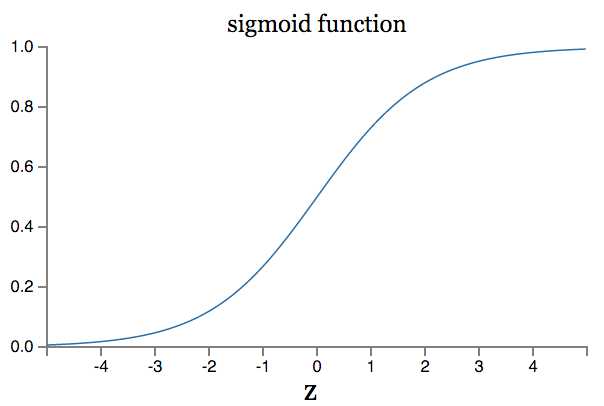
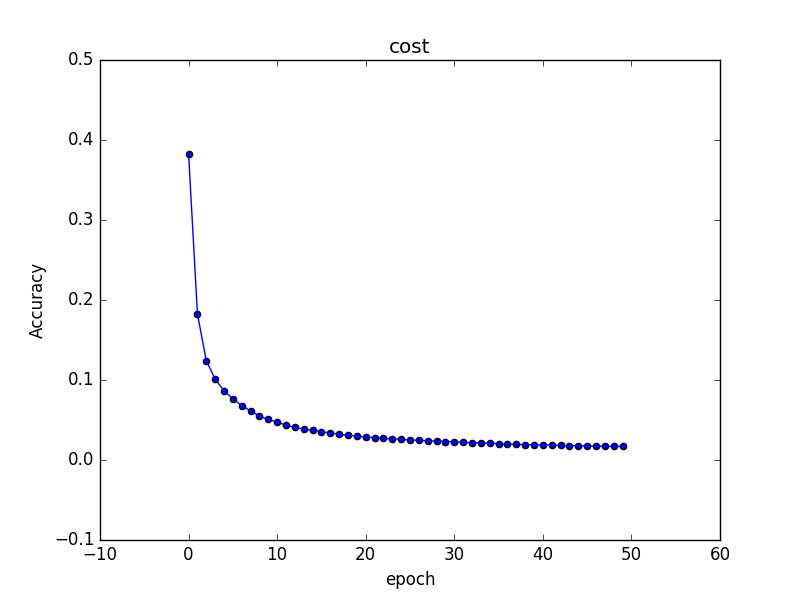
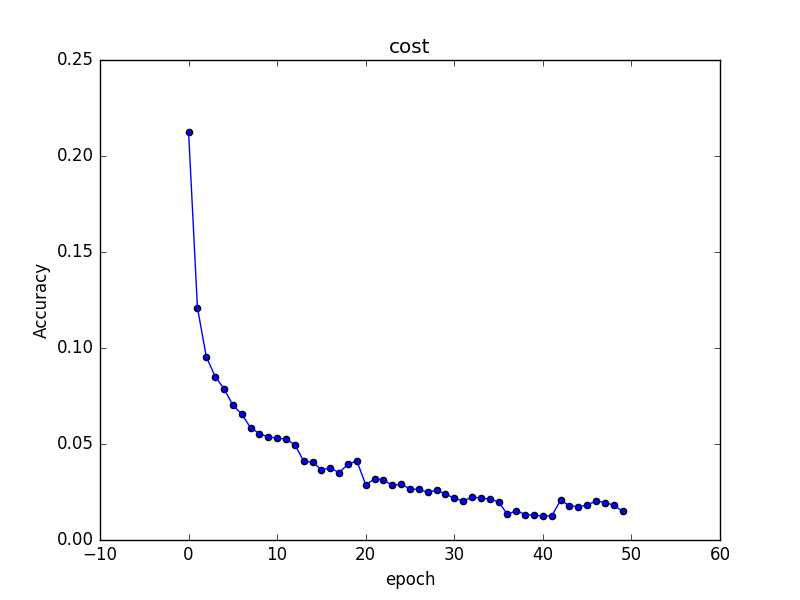
当神经元的输出接近 1时,曲线变得相当平,即σ′(z)的值会很小,进而也就使?C/?w和?C/?b会非常小。造成学习缓慢,下面有一个二次代价函数的cost变化图,epoch从15到50变化很小。
针对上述问题,希望对输出层选择一个不包含sigmoid的权值更新,使得
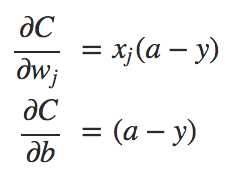
由链式法则,得到
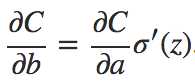
由σ′(z) = σ(z)(1? σ(z))以及σ(z)=a,可以将上式转换成
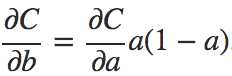
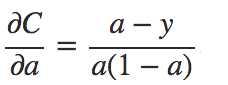
对方程进行关于a的积分,可得
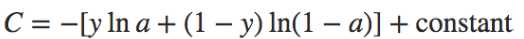
对样本进行平均之后就是下面的交叉熵代价函数
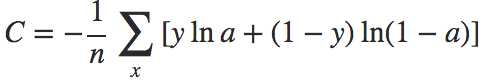
对比之前的输出层delta,相当于去掉了前面的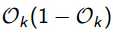
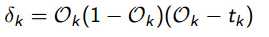
相应的代码仅改动了一行(58->59),新的cost变化图如下。
在训练和测试数据各5000个时,识别正确数从4347稍提高到4476。
1 # coding:utf8 2 import cPickle 3 import numpy as np 4 import matplotlib.pyplot as plt 5 6 7 class Network(object): 8 def __init__(self, sizes): 9 self.num_layers = len(sizes) 10 self.sizes = sizes 11 self.biases = [np.random.randn(y, 1) for y in sizes[1:]] # L(n-1)->L(n) 12 self.weights = [np.random.randn(y, x) 13 for x, y in zip(sizes[:-1], sizes[1:])] 14 15 def feedforward(self, a): 16 for b_, w_ in zip(self.biases, self.weights): 17 a = self.sigmoid(np.dot(w_, a)+b_) 18 return a 19 20 def SGD(self, training_data, test_data,epochs, mini_batch_size, eta): 21 n_test = len(test_data) 22 n = len(training_data) 23 plt.xlabel(‘epoch‘) 24 plt.ylabel(‘Accuracy‘) 25 plt.title(‘cost‘) 26 cy=[] 27 cx=range(epochs) 28 for j in cx: 29 self.cost = 0.0 30 np.random.shuffle(training_data) # shuffle 31 for k in xrange(0, n, mini_batch_size): 32 mini_batch = training_data[k:k+mini_batch_size] 33 self.update_mini_batch(mini_batch, eta) 34 cy.append(self.cost/n) 35 print "Epoch {0}: {1} / {2}".format( 36 j, self.evaluate(test_data), n_test) 37 plt.plot(cx,cy) 38 plt.scatter(cx,cy) 39 plt.show() 40 41 def update_mini_batch(self, mini_batch, eta): 42 for x, y in mini_batch: 43 delta_b, delta_w,cost = self.backprop(x, y) 44 self.weights -= eta/len(mini_batch)*delta_w 45 self.biases -= eta/len(mini_batch)*delta_b 46 self.cost += cost 47 48 def backprop(self, x, y): 49 b=np.zeros_like(self.biases) 50 w=np.zeros_like(self.weights) 51 a_ = x 52 a = [x] 53 for b_, w_ in zip(self.biases, self.weights): 54 a_ = self.sigmoid(np.dot(w_, a_)+b_) 55 a.append(a_) 56 for l in xrange(1, self.num_layers): 57 if l==1: 58 # delta= self.sigmoid_prime(a[-1])*(a[-1]-y) # O(k)=a[-1], t(k)=y 59 delta= a[-1]-y # cross-entropy 60 else: 61 sp = self.sigmoid_prime(a[-l]) # O(j)=a[-l] 62 delta = np.dot(self.weights[-l+1].T, delta) * sp 63 b[-l] = delta 64 w[-l] = np.dot(delta, a[-l-1].T) 65 cost=0.5*np.sum((a[-1]-y)**2) 66 return (b, w,cost) 67 68 def evaluate(self, test_data): 69 test_results = [(np.argmax(self.feedforward(x)), y) 70 for (x, y) in test_data] 71 return sum(int(x == y) for (x, y) in test_results) 72 73 def sigmoid(self,z): 74 return 1.0/(1.0+np.exp(-z)) 75 76 def sigmoid_prime(self,z): 77 return z*(1-z) 78 79 if __name__ == ‘__main__‘: 80 81 def get_label(i): 82 c=np.zeros((10,1)) 83 c[i]=1 84 return c 85 86 def get_data(data): 87 return [np.reshape(x, (784,1)) for x in data[0]] 88 89 f = open(‘mnist.pkl‘, ‘rb‘) 90 training_data, validation_data, test_data = cPickle.load(f) 91 training_inputs = get_data(training_data) 92 training_label=[get_label(y_) for y_ in training_data[1]] 93 data = zip(training_inputs,training_label) 94 test_inputs = training_inputs = get_data(test_data) 95 test = zip(test_inputs,test_data[1]) 96 net = Network([784, 30, 10]) 97 net.SGD(data[:5000],test[:5000],50,10, 3.0,) # 4476/5000 (4347/5000)
标签:alt result 对比 测试数据 变化 range layer png 1.0
原文地址:http://www.cnblogs.com/qw12/p/6107553.html