标签:tar 应该 转换 特征 pre 参数初始化 auth 调用顺序 splay
关键词:OpenCV::solvePnP
文章类型:方法封装、测试
@Author:VShawn(singlex@foxmail.com)
@Date:2016-11-27
@Lab: CvLab202@CSU
今天给大家带来的是一篇关于程序功能、性能测试的文章,读过《相机位姿估计1:根据四个特征点估计相机姿态》一文的同学应该会发现,直接使用OpenCV的solvePnP来估计相机位姿,在程序调用上相当麻烦,从一开始的参数设定到最后将计算出的矩阵转化为相机的位姿参数,需要花费近两百行代码。因此为了更方便地调用程序,今天我就给大家带来一个我自己对solvePnP的封装类PNPSolver,顺便将OpenCV自带的三种求解方法测试一遍。
封装的思路我就不写了,由于博客更新速度赶不上我写程序的速度,现在发上来的类已经修改过好几次了,思路也换了几次。不过大的方向没变,目的就是只需要输入参数,输入坐标点后直接可以得到相机在世界坐标系的坐标。
类的调用顺序:
1.初始化PNPSolver类;
2.调用SetCameraMatrix(),SetDistortionCoefficients()设置好相机内参数与镜头畸变参数;
3.向Points3D,Points2D中添加一一对应的特征点对;
4.调用Solve()方法运行计算;
5.从属性Theta_C2W中提取旋转角,从Position_OcInW中提取出相机在世界坐标系下的坐标。
以下是类体:
PNPSolver.h
#pragma once
#include <opencv2\opencv.hpp>
#include <math.h>
#include <iostream>
#include <fstream>
using namespace std;
// 本类用于快速解决PNP问题,顺带解决空间绕轴旋转以及图像系、相机系、世界系三系坐标投影问题
// 默认使用Gao的P3P+重投影法,要求输入4个特征点
// 调用顺序:
// 1.初始化本类
// 2.调用SetCameraMatrix(),SetDistortionCoefficients()设置好相机内参数与镜头畸变参数
// 3.向Points3D,Points2D中添加一一对应的特征点对
// 4.调用Solve()方法运行计算
// 5.从RoteM, TransM, W2CTheta等属性中提出结果
//
// 原理参见:http://www.cnblogs.com/singlex/category/911880.html
// Author:VShawn
// Ver:2016.11.25.0
class PNPSolver
{
public:
PNPSolver();
//带参数初始化
PNPSolver(double fx, double fy, double u0, double v0, double k_1, double k_2, double p_1, double p_2, double k_3);
~PNPSolver();
enum METHOD
{
CV_ITERATIVE = CV_ITERATIVE,
CV_P3P = CV_P3P,
CV_EPNP = CV_EPNP
};
/***********************位姿估计所用特征点**************************/
vector<cv::Point3f> Points3D;//存储四个点的世界坐标
vector<cv::Point2f> Points2D;//存储四个点的图像坐标
/***********************位姿估计结果**************************/
//最后求出的旋转矩阵与平移矩阵
cv::Mat RoteM, TransM;
//世界系到相机系的三轴旋转欧拉角,世界系照此旋转后可以与相机坐标系完全平行。
//旋转顺序为x、y、z
cv::Point3f Theta_W2C;
//相机系到世界系的三轴旋转欧拉角,相机坐标系照此旋转后可以与世界坐标系完全平行。
//旋转顺序为z、y、x
cv::Point3f Theta_C2W;
//相机坐标系中,世界坐标系原点Ow的坐标
cv::Point3f Position_OwInC;
//世界坐标系中,相机坐标系原点Oc的坐标
cv::Point3f Position_OcInW;
/*********************公有方法*****************************/
//解PNP问题,获得位姿信息
//调用后在RoteM, TransM, W2CTheta等属性中提取计算结果,属性说明参见注释
//输出参数:CV_ITERATIVE,CV_P3P(默认),CV_EPNP,具体参见Opencv documentation.
//实测
//CV_ITERATIVE迭代法似乎只能用4个共面特征点求解,5个点或非共面4点解不出正确的解
//CV_P3P的Gao的方法可以使用任意四个特征点,特征点数量不能少于4也不能多于4
//CV_EPNP方法可以实现特征点数>=4的问题求解,不需要4点共面
//返回值:
//0正确
//-1相机内参数或畸变参数未设置
//-2未提供足够的特征点,或特征点数目不匹配
//-3输入的点数据有误,详见printf信息
int Solve(METHOD method = METHOD::CV_P3P);
//根据计算出的结果将世界坐标重投影到图像,返回像素坐标点集
//使用前需要先用Solve()解出相机位姿
//输入为世界坐标系的点坐标集合
//输出为点投影到图像上的图像坐标集合
vector<cv::Point2f> WordFrame2ImageFrame(vector<cv::Point3f> WorldPoints);
//根据输入的参数将图像坐标转换到相机坐标中
//使用前需要先用Solve()解出相机位姿
//输入为图像上的点坐标
//double F为镜头焦距
//输出为点在焦距=F时的相机坐标系坐标
cv::Point3f ImageFrame2CameraFrame(cv::Point2f p, double F);
//设置相机内参数矩阵
void SetCameraMatrix(double fx, double fy, double u0, double v0)
{
camera_matrix = cv::Mat(3, 3, CV_64FC1, cv::Scalar::all(0));
camera_matrix.ptr<double>(0)[0] = fx;
camera_matrix.ptr<double>(0)[2] = u0;
camera_matrix.ptr<double>(1)[1] = fy;
camera_matrix.ptr<double>(1)[2] = v0;
camera_matrix.ptr<double>(2)[2] = 1.0f;
}
//设置畸变系数矩阵
void SetDistortionCoefficients(double k_1, double k_2, double p_1, double p_2, double k_3)
{
distortion_coefficients = cv::Mat(5, 1, CV_64FC1, cv::Scalar::all(0));
distortion_coefficients.ptr<double>(0)[0] = k_1;
distortion_coefficients.ptr<double>(1)[0] = k_2;
distortion_coefficients.ptr<double>(2)[0] = p_1;
distortion_coefficients.ptr<double>(3)[0] = p_2;
distortion_coefficients.ptr<double>(4)[0] = k_3;
}
/********************公有静态方法*********************/
//点绕任意向量旋转,右手系
static cv::Point3f RotateByVector(double old_x, double old_y, double old_z, double vx, double vy, double vz, double theta)
{
double r = theta * CV_PI / 180;
double c = cos(r);
double s = sin(r);
double new_x = (vx*vx*(1 - c) + c) * old_x + (vx*vy*(1 - c) - vz*s) * old_y + (vx*vz*(1 - c) + vy*s) * old_z;
double new_y = (vy*vx*(1 - c) + vz*s) * old_x + (vy*vy*(1 - c) + c) * old_y + (vy*vz*(1 - c) - vx*s) * old_z;
double new_z = (vx*vz*(1 - c) - vy*s) * old_x + (vy*vz*(1 - c) + vx*s) * old_y + (vz*vz*(1 - c) + c) * old_z;
return cv::Point3f(new_x, new_y, new_z);
}
//将空间点绕Z轴旋转
//输入参数 x y为空间点原始x y坐标
//thetaz为空间点绕Z轴旋转多少度,角度制范围在-180到180
//outx outy为旋转后的结果坐标
static void CodeRotateByZ(double x, double y, double thetaz, double& outx, double& outy)
{
double x1 = x;//将变量拷贝一次,保证&x == &outx这种情况下也能计算正确
double y1 = y;
double rz = thetaz * CV_PI / 180;
outx = cos(rz) * x1 - sin(rz) * y1;
outy = sin(rz) * x1 + cos(rz) * y1;
}
//将空间点绕Y轴旋转
//输入参数 x z为空间点原始x z坐标
//thetay为空间点绕Y轴旋转多少度,角度制范围在-180到180
//outx outz为旋转后的结果坐标
static void CodeRotateByY(double x, double z, double thetay, double& outx, double& outz)
{
double x1 = x;
double z1 = z;
double ry = thetay * CV_PI / 180;
outx = cos(ry) * x1 + sin(ry) * z1;
outz = cos(ry) * z1 - sin(ry) * x1;
}
//将空间点绕X轴旋转
//输入参数 y z为空间点原始y z坐标
//thetax为空间点绕X轴旋转多少度,角度制,范围在-180到180
//outy outz为旋转后的结果坐标
static void CodeRotateByX(double y, double z, double thetax, double& outy, double& outz)
{
double y1 = y;//将变量拷贝一次,保证&y == &y这种情况下也能计算正确
double z1 = z;
double rx = thetax * CV_PI / 180;
outy = cos(rx) * y1 - sin(rx) * z1;
outz = cos(rx) * z1 + sin(rx) * y1;
}
private:
cv::Mat camera_matrix;//内参数矩阵
cv::Mat distortion_coefficients;//畸变系数
cv::Mat rvec;//解出来的旋转向量
cv::Mat tvec;//解出来的平移向量
};
PNPSolver.cpp
#include "PNPSolver.h"
// 本类用于快速解决PNP问题,顺带解决空间绕轴旋转以及图像系、相机系、世界系三系坐标投影问题
// 调用顺序:
// 1.初始化本类
// 2.调用SetCameraMatrix(),SetDistortionCoefficients()设置好相机内参数与镜头畸变参数
// 3.向Points3D,Points2D中添加一一对应的特征点对
// 4.调用Solve()方法运行计算
// 5.从RoteM, TransM, W2CTheta等属性中提出结果
//
// 原理参见:http://www.cnblogs.com/singlex/category/911880.html
// Author:VShawn
// Ver:2016.11.26.0
PNPSolver::PNPSolver()
{
//初始化输出矩阵
vector<double> rv(3), tv(3);
cv::Mat rvec(rv), tvec(tv);
}
PNPSolver::PNPSolver(double fx, double fy, double u0, double v0, double k_1, double k_2, double p_1, double p_2, double k_3)
{
//初始化输出矩阵
vector<double> rv(3), tv(3);
cv::Mat rvec(rv), tvec(tv);
SetCameraMatrix(fx, fy, u0, v0);
SetDistortionCoefficients(k_1, k_2, p_1, p_2, k_3);
}
PNPSolver::~PNPSolver()
{
}
int PNPSolver::Solve(METHOD method)
{
//数据校验
if (camera_matrix.cols == 0 || distortion_coefficients.cols == 0)
{
printf("ErrCode:-1,相机内参数或畸变参数未设置!\r\n");
return -1;
}
if (Points3D.size() != Points2D.size())
{
printf("ErrCode:-2,3D点数量与2D点数量不一致!\r\n");
return -2;
}
if (method == METHOD::CV_P3P || method == METHOD::CV_ITERATIVE)
{
if (Points3D.size() != 4)
{
printf("ErrCode:-2,使用CV_ITERATIVE或CV_P3P方法时输入的特征点数量应为4!\r\n");
return -2;
}
}
else
{
if (Points3D.size() < 4)
{
printf("ErrCode:-2,输入的特征点数量应大于4!\r\n");
return -2;
}
}
////TODO::检验是否是共面的四点
//if ((method == METHOD::CV_ITERATIVE || method == METHOD::CV_EPNP) && Points2D.size() == 4)
//{
// //通过向量两两叉乘获得法向量,看法向量是否平行
//}
/*******************解决PNP问题*********************/
//有三种方法求解
solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, method); //实测迭代法似乎只能用共面特征点求位置
//solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_ITERATIVE); //实测迭代法似乎只能用共面特征点求位置
//solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_P3P); //Gao的方法可以使用任意四个特征点
//solvePnP(Points3D, Points2D, camera_matrix, distortion_coefficients, rvec, tvec, false, CV_EPNP);
/*******************提取旋转矩阵*********************/
double rm[9];
RoteM = cv::Mat(3, 3, CV_64FC1, rm);
Rodrigues(rvec, RoteM);
double r11 = RoteM.ptr<double>(0)[0];
double r12 = RoteM.ptr<double>(0)[1];
double r13 = RoteM.ptr<double>(0)[2];
double r21 = RoteM.ptr<double>(1)[0];
double r22 = RoteM.ptr<double>(1)[1];
double r23 = RoteM.ptr<double>(1)[2];
double r31 = RoteM.ptr<double>(2)[0];
double r32 = RoteM.ptr<double>(2)[1];
double r33 = RoteM.ptr<double>(2)[2];
TransM = tvec;
//计算出相机坐标系的三轴旋转欧拉角,旋转后可以转出世界坐标系。
//旋转顺序为z、y、x
double thetaz = atan2(r21, r11) / CV_PI * 180;
double thetay = atan2(-1 * r31, sqrt(r32*r32 + r33*r33)) / CV_PI * 180;
double thetax = atan2(r32, r33) / CV_PI * 180;
//相机系到世界系的三轴旋转欧拉角,相机坐标系照此旋转后可以与世界坐标系完全平行。
//旋转顺序为z、y、x
Theta_C2W.z = thetaz;
Theta_C2W.y = thetay;
Theta_C2W.x = thetax;
//计算出世界系到相机系的三轴旋转欧拉角,世界系照此旋转后可以转出相机坐标系。
//旋转顺序为x、y、z
Theta_W2C.x = -1 * thetax;
Theta_W2C.y = -1 * thetay;
Theta_W2C.z = -1 * thetaz;
/*************************************此处计算出相机坐标系原点Oc在世界坐标系中的位置**********************************************/
/***********************************************************************************/
/* 当原始坐标系经过旋转z、y、x三次旋转后,与世界坐标系平行,向量OcOw会跟着旋转 */
/* 而我们想知道的是两个坐标系完全平行时,OcOw的值 */
/* 因此,原始坐标系每次旋转完成后,对向量OcOw进行一次反相旋转,最终可以得到两个坐标系完全平行时的OcOw */
/* 该向量乘以-1就是世界坐标系下相机的坐标 */
/***********************************************************************************/
//提出平移矩阵,表示从相机坐标系原点,跟着向量(x,y,z)走,就到了世界坐标系原点
double tx = tvec.ptr<double>(0)[0];
double ty = tvec.ptr<double>(0)[1];
double tz = tvec.ptr<double>(0)[2];
//x y z 为唯一向量在相机原始坐标系下的向量值
//也就是向量OcOw在相机坐标系下的值
double x = tx, y = ty, z = tz;
Position_OwInC.x = x;
Position_OwInC.y = y;
Position_OwInC.z = z;
//进行三次反向旋转
CodeRotateByZ(x, y, -1 * thetaz, x, y);
CodeRotateByY(x, z, -1 * thetay, x, z);
CodeRotateByX(y, z, -1 * thetax, y, z);
//获得相机在世界坐标系下的位置坐标
//即向量OcOw在世界坐标系下的值
Position_OcInW.x = x*-1;
Position_OcInW.y = y*-1;
Position_OcInW.z = z*-1;
return 0;
}
//根据计算出的结果将世界坐标重投影到图像,返回像素坐标点集
//输入为世界坐标系的点坐标集合
//输出为点投影到图像上的图像坐标集合
vector<cv::Point2f> PNPSolver::WordFrame2ImageFrame(vector<cv::Point3f> WorldPoints)
{
vector<cv::Point2f> projectedPoints;
cv::projectPoints(WorldPoints, rvec, tvec, camera_matrix, distortion_coefficients, projectedPoints);
return projectedPoints;
}
//根据输入的参数将图像坐标转换到相机坐标中
//使用前需要先用Solve()解出相机位姿
//输入为图像上的点坐标
//double F为镜头焦距
//输出为点在焦距=F时的相机坐标系坐标
cv::Point3f PNPSolver::ImageFrame2CameraFrame(cv::Point2f p, double F)
{
double fx;
double fy;
double u0;
double v0;
fx = camera_matrix.ptr<double>(0)[0];
u0 = camera_matrix.ptr<double>(0)[2];
fy = camera_matrix.ptr<double>(1)[1];
v0 = camera_matrix.ptr<double>(1)[2];
double zc = F;
double xc = (p.x - u0)*F / fx;
double yc = (p.y - v0)*F / fy;
return cv::Point3f(xc, yc, zc);
}
一个典型的调用示例
//初始化PNPSolver类 PNPSolver p4psolver; //初始化相机参数 p4psolver.SetCameraMatrix(fx, fy, u0, v0); //设置畸变参数 p4psolver.SetDistortionCoefficients(k1, k2, p1, p2, k3); p4psolver.Points3D.push_back(cv::Point3f(0, 0, 0)); //P1三维坐标的单位是毫米 p4psolver.Points3D.push_back(cv::Point3f(0, 200, 0)); //P2 p4psolver.Points3D.push_back(cv::Point3f(150, 0, 0)); //P3 //p4psolver.Points3D.push_back(cv::Point3f(150, 200, 0)); //P4 p4psolver.Points3D.push_back(cv::Point3f(0, 100, 105)); //P5 cout << "test2:特征点世界坐标 = " << endl << p4psolver.Points3D << endl; p4psolver.Points2D.push_back(cv::Point2f(2985, 1688)); //P1 p4psolver.Points2D.push_back(cv::Point2f(5081, 1690)); //P2 p4psolver.Points2D.push_back(cv::Point2f(2997, 2797)); //P3 //p4psolver.Points2D.push_back(cv::Point2f(5544, 2757)); //P4 p4psolver.Points2D.push_back(cv::Point2f(4148, 673)); //P5 cout << "test2:图中特征点坐标 = " << endl << p4psolver.Points2D << endl; if (p4psolver.Solve(PNPSolver::METHOD::CV_P3P) == 0) cout << "test2:CV_P3P方法: 相机位姿→" << "Oc坐标=" << p4psolver.Position_OcInW << " 相机旋转=" << p4psolver.Theta_W2C << endl; if (p4psolver.Solve(PNPSolver::METHOD::CV_ITERATIVE) == 0) cout << "test2:CV_ITERATIVE方法: 相机位姿→" << "Oc坐标=" << p4psolver.Position_OcInW << " 相机旋转=" << p4psolver.Theta_W2C << endl; if (p4psolver.Solve(PNPSolver::METHOD::CV_EPNP) == 0) cout << "test2:CV_EPNP方法: 相机位姿→" << "Oc坐标=" << p4psolver.Position_OcInW << " 相机旋转=" << p4psolver.Theta_W2C << endl;
OpenCV提供了三种方法进行PNP计算,三种方法具体怎么计算的就请各位自己查询opencv documentation以及相关的论文了,我看了个大概然后结合自己实际的测试情况给出一个结论,不一定正确,仅供参考:
|
方法名 |
说明 |
测试结论 |
|
CV_P3P |
这个方法使用非常经典的Gao方法解P3P问题,求出4组可能的解,再通过对第四个点的重投影,返回重投影误差最小的点。 |
可以使用任意4个特征点求解,不要共面,特征点数量不为4时报错 |
|
CV_ITERATIVE |
该方法基于Levenberg-Marquardt optimization迭代求解PNP问题,实质是迭代求出重投影误差最小的解,这个解显然不一定是正解。 实测该方法只有用4个共面的特征点时才能求出正确的解,使用5个特征点或4点非共面的特征点都得不到正确的位姿。 |
只能用4个共面的特征点来解位姿 |
|
CV_EPNP |
该方法使用EfficientPNP方法求解问题,具体怎么做的当时网速不好我没下载到论文,后面又懒得去看了。 |
对于N个特征点,只要N>3就能够求出正解。 |
测试截图:
1.使用四个共面的特征点,显然三种方法都能得到正解,但相互之间略有误差。
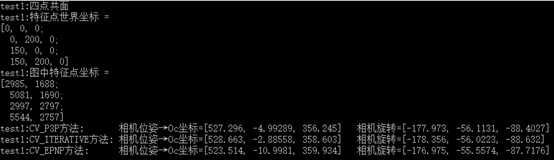
2使用四个非共面的特征点,CV_ITERATIVE方法解错了。
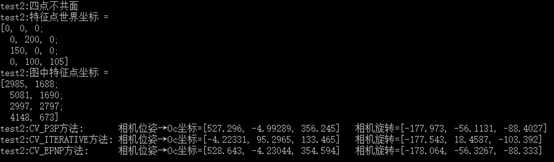
3.使用5个特征点求解,只有CV_EPNP能够用

最后对三种方法的性能进行测试,通过对test1重复执行1000次获得算法的运行时间,从结果可以看出迭代法显然是最慢的,Gao的P3P+重投影法用时最少,EPNP法其次。

综合以上的测试,推荐使用CV_P3P来解决实际问题,该方法对于有四个特征点的情况限制少、运算速度快。当特征点数大于4时,可以取多组4特征点计算出结果再求平均值,或者为了简单点就直接使用CV_EPNP法。
不推荐使用CV_ITERATIVE方法。
程序下载地址:Github
相机位姿估计1_1:OpenCV:solvePnP二次封装与性能测试
标签:tar 应该 转换 特征 pre 参数初始化 auth 调用顺序 splay
原文地址:http://www.cnblogs.com/singlex/p/pose_estimation_1_1.html