标签：hdu   凸包   

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1392

Surround the Trees

There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him? 
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.



There are no more than 100 trees.

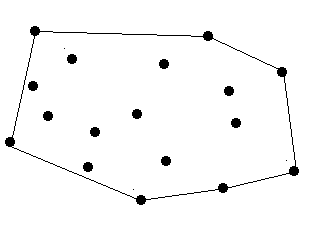
9 
12 7 
24 9 
30 5 
41 9 
80 7 
50 87 
22 9 
45 1 
50 7 
0 

243.06

代码如下：

//#pragma warning (disable:4786)
#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#include <cstdlib>
#include <climits>
#include <ctype.h>
#include <queue>
#include <stack>
#include <vector>
#include <utility>
#include <deque>
#include <set>
#include <map>
#include <iostream>
#include <algorithm>
using namespace std;
const double eps = 1e-9;
//const double pi = atan(1.0)*4;
const double pi = 3.1415926535897932384626;
#define INF 1e18
//typedef long long LL;
//typedef __int64 LL;
const int MAXN = 1017;

struct point
{
    int x,y;
} e[MAXN],res[MAXN]; //坐标点集，位于凸包上的点

bool cmp(point a,point b)//排序方法
{
    if(a.x == b.x)
        return a.y < b.y;
    return a.x < b.x;
}

int cross(point a,point b,point c)//叉积（向量积）
{
    return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);
}

double lenght(point a,point b)//距离
{
    return sqrt(1.0*(a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

int convex(int n)//求凸包上的点
{
    sort(e,e+n,cmp);
    int m=0, i, k;
    //求得下凸包，逆时针
    //已知凸包点m个，如果新加入点为i，则向量(m-2,i)必定要在(m-2,m-1)的逆时针方向才符合凸包的性质
    //若不成立，则m-1点不在凸包上。
    for(i = 0; i < n; i++)
    {
        while(m>1 && cross(res[m-1],e[i],res[m-2])<=0)
            m--;
        res[m++]=e[i];
    }
    k = m;
    //求得上凸包
    for(i = n-2; i >= 0; i--)
    {
        while(m>k && cross(res[m-1],e[i],res[m-2])<=0)
            m--;
        res[m++]=e[i];
    }
    if(n > 1)//起始点重复。
        m--;
    return m;
}

int main()
{
    int n, m;
    while(~scanf("%d",&n) && n)
    {
        for(int i = 0; i < n; i++)
            scanf("%d%d",&e[i].x,&e[i].y);
        m = convex(n);
        double ans = 0;
        for(int i = 1; i < m; i++)//求凸包的周长
            ans+=lenght(res[i],res[i-1]);
        ans+=lenght(res[m-1],res[0]);//首尾相接
        if(n == 2)
            ans/=2.0;
        printf("%.2lf\n",ans);
    }
    return 0;
}

hdu 1392 Surround the Trees（凸包果题）,布布扣,bubuko.com

hdu 1392 Surround the Trees（凸包果题）

标签：hdu   凸包   

原文地址：http://blog.csdn.net/u012860063/article/details/38614107