标签:com blog alt src 核函数 复杂 idt 时间 利用
1. 核技巧引入
如果要用SVM来做非线性的分类,我们采用的方法是将原来的特征空间映射到另一个更高维的空间,在这个更高维的空间做线性的SVM。即:
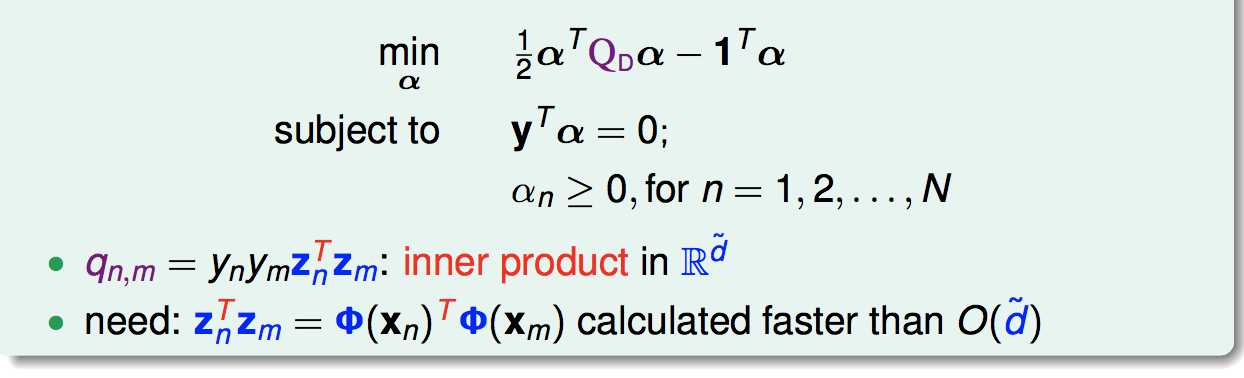
在这里我们计算这个向量内积有两种方法:一种是对Φ(x)给出明确的定义,分别算出两个高维向量,再做内积;另一种就是利用核函数,直接算出高维的内积。我们以一个例子来看这两种方法,定义一个二次转化:

我们可以直接计算出内积:
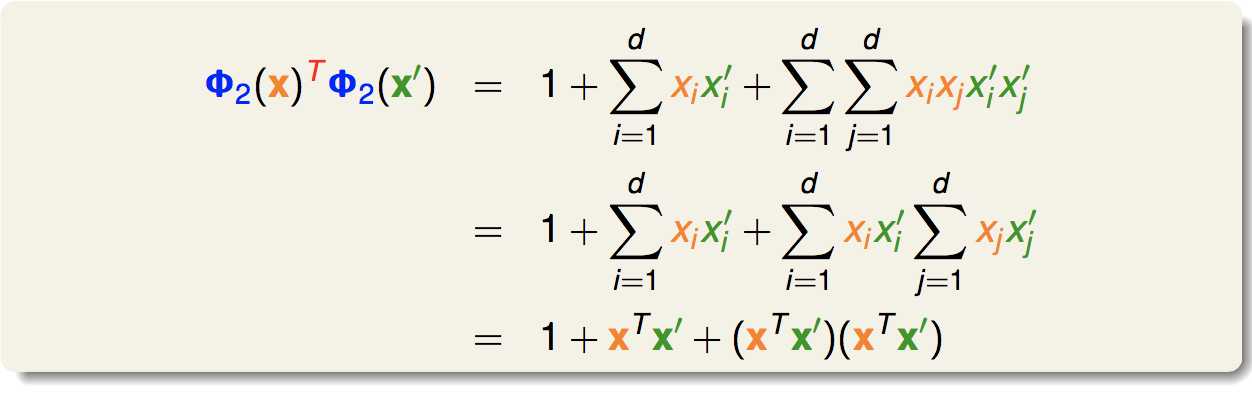
可以看出,最后的结果能够用x和x一撇表示出来,这就是一个核函数:

在这里,我们是给出了一个Φ(x)来推出它的核函数。但事实上,我们可以直接给一个核函数(只要我们能证明它是一个核函数),而不用知道它对应的Φ(x)是什么。这样做的一个好处就是我们不用求出高维向量在做内积,可以通过形式简单的核函数直接计算内积,计算复杂度降低了,到后面我们用核函数甚至可以引入无限维的转换。
我们的b值就是:
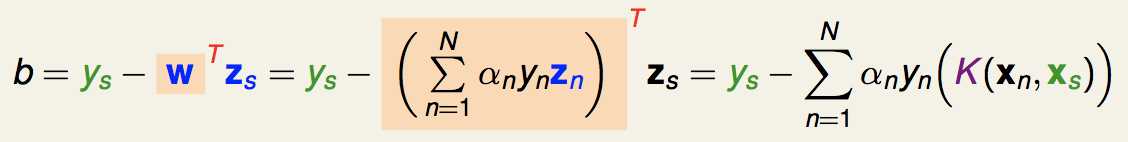
最终得到的分离超平面就是:
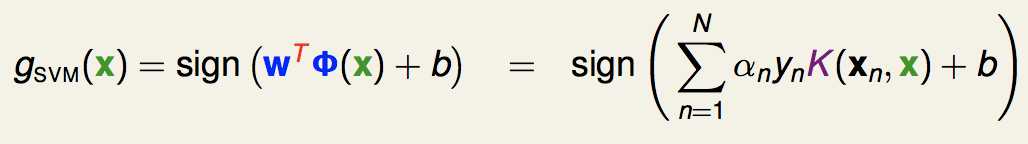
可以看出,不管是求解的优化问题还是最后的模型,我们都可以用核函数来表示。(这里我们不用知道w是什么)
因此,通过核函数的引入,我们相当于隐式的在高维空间进行线性SVM,而不用知道低维到高维的具体映射是什么。
关于使用核函数后的时间复杂度的优化,如下:

2 多项式核函数
首先对一个常用的核函数——二次多项式核函数做导出:
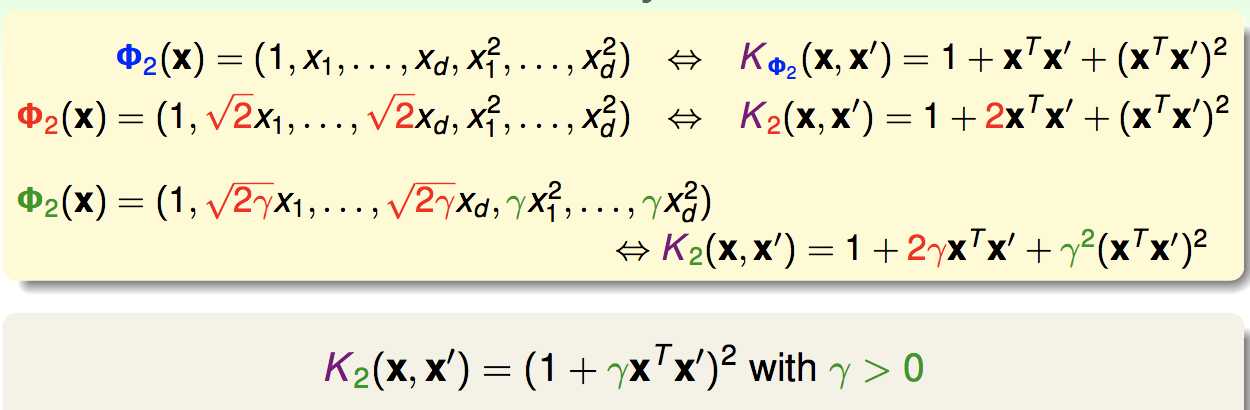
对于不同的二次核,我们产生的决策边界是不同的:
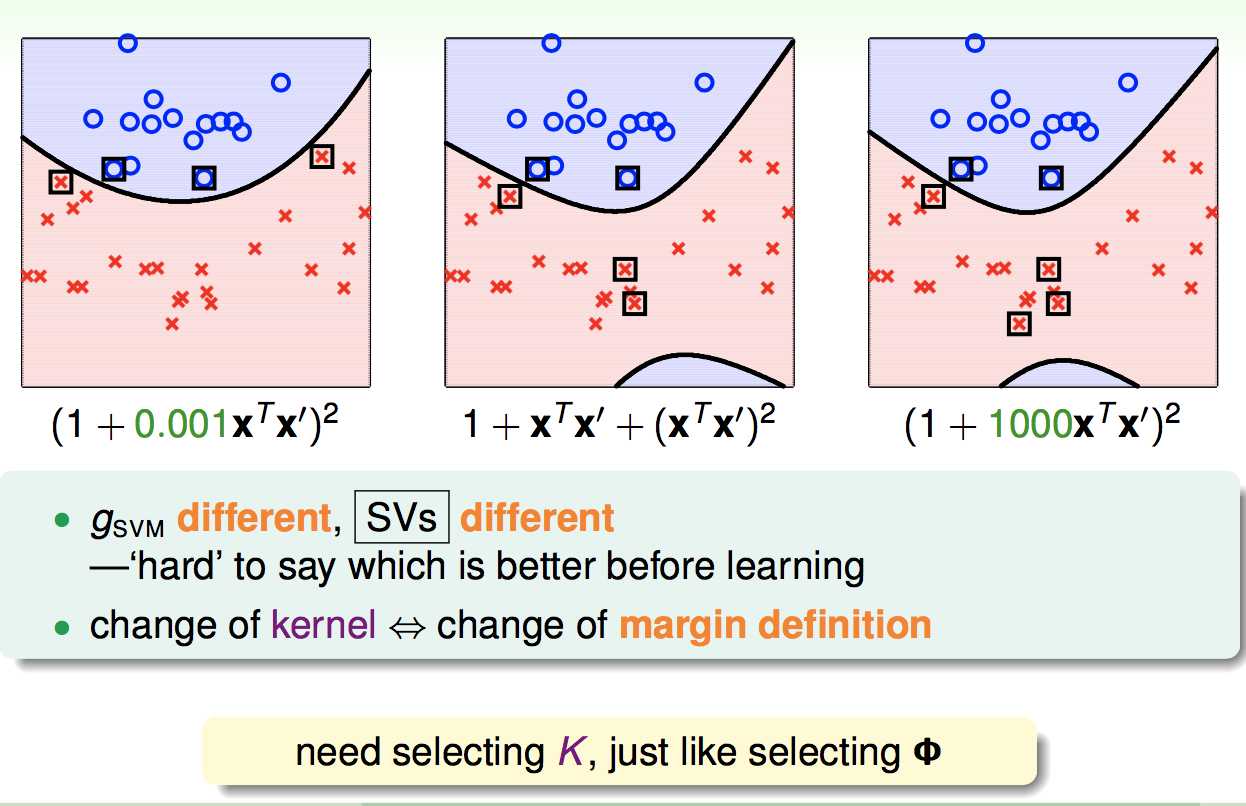
之后我们可以推广出通用的多项式核函数:

标签:com blog alt src 核函数 复杂 idt 时间 利用
原文地址:http://www.cnblogs.com/coldyan/p/6142378.html