标签：lin 应该 标准 png 分割 算法 变换 连线 进一步
接下来的讨论假设数据都是线性可分的。
假设有训练数据和分类西线如下图所示：
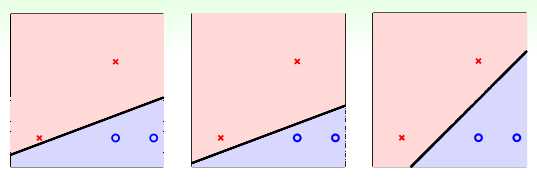
很明显，三个分类器都能够正确分类训练数据，但是哪一个的效果更改呢？直觉告诉我们第三个，为什么呢？
这是因为第三个的那些点离分割超平面的距离较远，这样能够容忍更大的噪声， 鲁棒性更强。
我们的目标是寻找分割超平面导致间隔最大化。形象的说我们定义分割超平面两边的点与分割超平面的最短距离为“fat”，那么，我们的目标就是需要寻找具有最大"fat‘‘的分割超平面。利用公式表示如下：
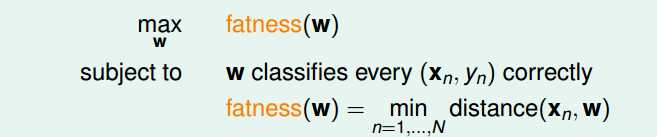
术语化描述就是间隔最大化：
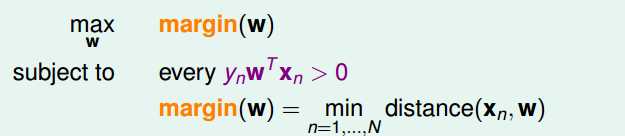
那么，怎么求解平面外一个点到一个平面的距离呢？这是高中学过的公式，简单推导如下：
假设平面方程为：
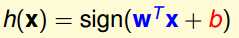sign()由样本属于正样本还是负样本确定。其实w就是超平面的法向量。
法向量w是垂直于平面的，所以平面外一点到平面的距离就是平面外一点与平面内一点的连线在法向量上的投影。
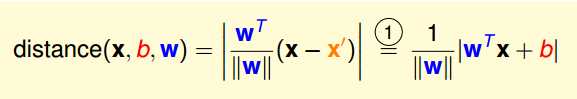
由于所有样本都正确分类，所以对每一个样本点，我们有 
带入上式得到：
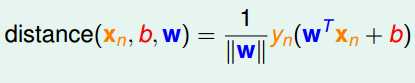
带入最开始的我们的目标问题得到：
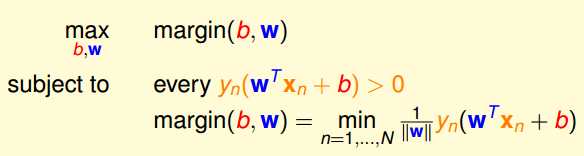
进一步处理，对方程归一化处理，得到：
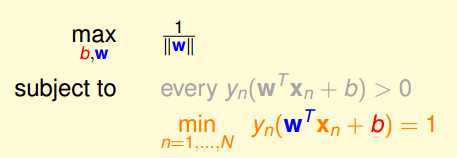
由于这一问题不方便求解，我们现在对条件进行放宽，把上式的最后一个条件转化为：
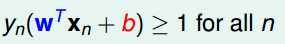
可以证明，这个条件的放宽仍然能够保证有最小值能够取到1，没有全部大于1的担忧。
因为假设放宽后所有的点都导致上式大于1,那么至少有一个最小值比如就取1.126吧，那么也就是得到
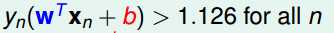
现在我两边同时除以1.126，发现我们能够找到刚好的wb的组合
，能够使得我们呢的目标函数更大，而你之前求得的这个wb就是最大的，所以矛盾。
另外，由于习惯问题或者函数库的问题，我们把目标函数取倒数变最大目标为最小目标。再进行一个平方，转化向量长度为向量内积，再乘上系数1/2。最终得到我们的目标函数及其限制条件为：
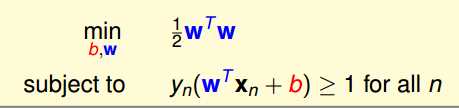
首先我们想到是不是可以使用梯度下降算法求解上述模型，但是由于加了那么多的条件的限制，所以这似乎走不通。
幸运的是，我们观察表达式发现，这是一个二次规划问题，（目标函数关于w,b的凸二次，限制条件关于w，b线性）
二次规划问题的求解可以直接调用有关库，但首先应该转化为标准形式：
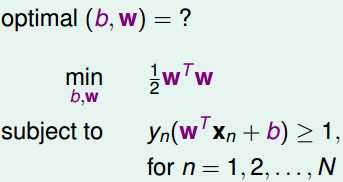
对比得到：
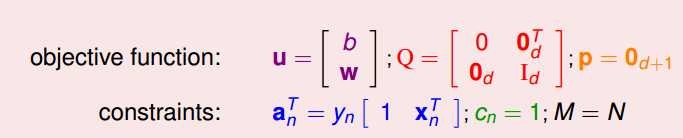
待补充...
之前我们讨论过Logestic回归的代价函数为：
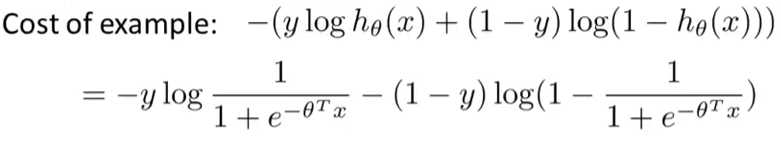
画出图来显示如下：
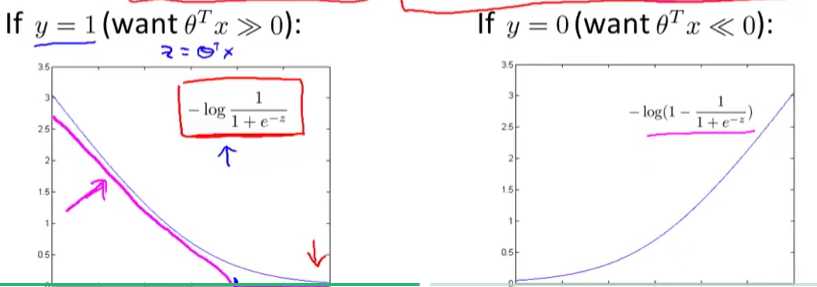
也可以看到，y = 1时，z >> 0 时，代价较小，另一边则代价较大。
y = 0时， z >> 0 时，代价较小，另一边则较大。
现在我们把上述曲线做一个近似，得到y=1时候的代价函数曲线和y=0时候的代价函数曲线。
相对应的，把之前的Logestic回归的代价函数转换：
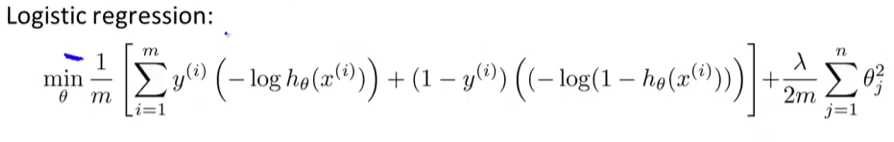
得到：
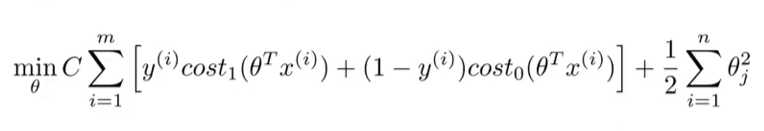
基于以上转换，我们得到：
我们发现，相比于逻辑回归，我们的要求似乎严格了。由大于等于0变为了大于等于1.
现在假设C特别大，我们有：
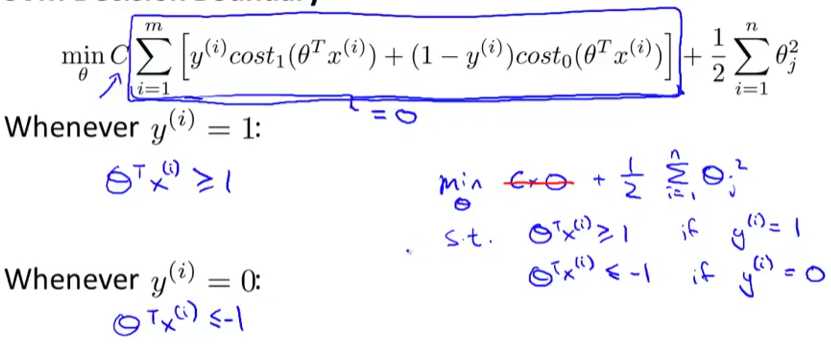
这样，就得到了和我们事前讨论的一样的目标函数及约束条件。
之前我们由Logestic慢慢变换得到
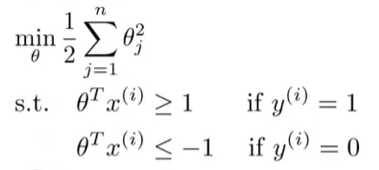
我们可以把最小化目标改为最小化||theta||，接下来假设是二维的并且theta0 = 0。
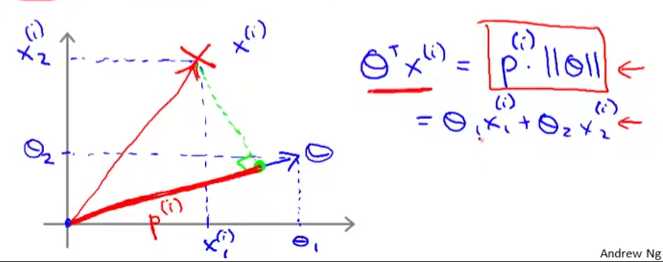
如图，样本点x(i)，参数theta,我们的约束条件需要x(i)与theta的内积的绝对值大于等于1,p(i)为x(i)在theta上的投影，也就是p(i)和theta长度的乘积大于等于1。
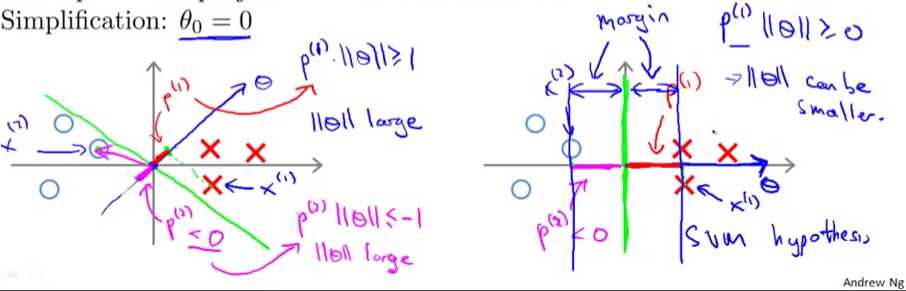
如上图所示，假设选择了左边的分界线，那么这些点在法向量theta上的投影p(i)就会比较小，相应的你theta的范数就会比较大，这和我们的目标函数最小化相悖，所以我们的决策函数不会选择这条分界线，相反会选择右边这个是的p(i)很大的分界线。
这就解释了为什么会上述目标函数的优化问题会选择大间隔分类器。
标签：lin 应该 标准 png 分割 算法 变换 连线 进一步
原文地址：http://www.cnblogs.com/futurehau/p/6143178.html
