标签:i++ max [] art nbsp http 复杂度 read sub
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 2102 | Accepted: 975 |
Description
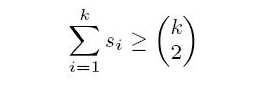
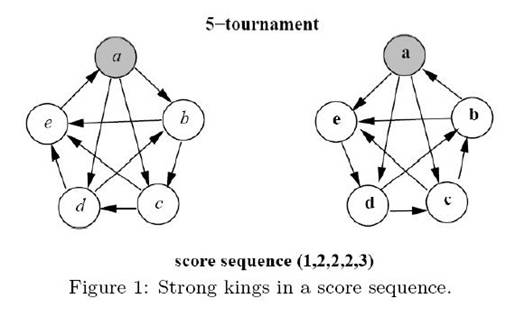
Input
Output
Sample Input
5 1 2 2 2 3 1 1 3 4 4 4 4 3 3 4 4 4 4 5 6 6 6 0 3 4 4 4 5 5 5 6 0 3 3 3 3 3
Sample Output
2 4 5 3 5
Source
网络流 最大流
将代表每场比赛的边记为流量图中的点,从S到每场比赛连边,容量为1;
从每个参赛者到T连边,容量为胜利场数。
假设king是胜场最多的前king个人,将参赛者a[]按胜利次数从大到小排序,方便连边。枚举或者二分king数量(n<=10,复杂度没啥差别),对于每场比赛,如果其中一方a是king,且另一方b胜场更多,那么将边强行定向,从比赛到a连边,容量为1(表示胜利);否则a和b都可以胜利,就将边看作双向边,比赛到a、b各连一条边,容量为1。
↑如果能跑满流,那么当前选取的king个数可行。
(测试数据格式似乎很诡异,以下代码中,如果读入方式换成注释掉的部分,本地手测都能过,交上去就WA)
刚开始有另一种设想:
将参赛者拆点,S到每个入点连边,容量为此人胜场a[i],每个出点到T连边,容量为此人负场n-1-a[i]。
枚举king的个数,每多加一个人,就在前一步的参量网络上添边,看网络流能否增广,能就继续加king人数。
但是这种算法在测discuss里的大数据时就挂掉了。
↑姑且记个思路。
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<vector> 7 #define LL long long 8 using namespace std; 9 const int mx[5]={0,1,0,-1,0}; 10 const int my[5]={0,0,1,0,-1}; 11 const int mxn=300; 12 int a[mxn],n=0; 13 int cmp(const int q,const int e){return q>e;} 14 void read(){ 15 char s[210]; 16 /* fgets(s,200,stdin); 17 int len=strlen(s); 18 for(int i=0;i<len;i++){ 19 int x=0,f=1;char ch=s[i]; 20 while(ch<‘0‘ || ch>‘9‘){if(ch==‘-‘)f=-1;ch=s[++i];} 21 while(ch>=‘0‘ && ch<=‘9‘){x=x*10+ch-‘0‘;ch=s[++i];} 22 a[++n]=x; 23 }*/ 24 gets(s); 25 int len=strlen(s); 26 for(int i=0;i<len;i++){ 27 if(s[i]>=‘0‘ && s[i]<=‘9‘)a[++n]=(s[i]-‘0‘); 28 } 29 return; 30 } 31 struct edge{int v,nxt,f;}e[mxn*mxn*2]; 32 int hd[mxn],mct=1; 33 inline void add_edge(int u,int v,int f){ 34 e[++mct].v=v;e[mct].f=f;e[mct].nxt=hd[u];hd[u]=mct;return; 35 } 36 inline void ins(int u,int v,int f){add_edge(u,v,f);add_edge(v,u,0);return;} 37 int S,T; 38 int id[30][30]; 39 int bct=0; 40 void init(){ 41 memset(hd,0,sizeof hd); 42 n=0;mct=1;bct=0; 43 return; 44 } 45 void init2(){ 46 for(int i=1;i<=n;i++) 47 for(int j=i+1;j<=n;j++) 48 id[i][j]=id[j][i]=++bct; 49 return; 50 } 51 int d[mxn]; 52 bool BFS(){ 53 memset(d,0,sizeof d); 54 queue<int>q; 55 d[S]=1; 56 q.push(S); 57 while(!q.empty()){ 58 int u=q.front();q.pop(); 59 for(int i=hd[u];i;i=e[i].nxt){ 60 int v=e[i].v; 61 if(!d[v] && e[i].f){ 62 d[v]=d[u]+1; 63 q.push(v); 64 } 65 } 66 } 67 return d[T]; 68 } 69 int DFS(int u,int lim){ 70 if(u==T)return lim; 71 int tmp,f=0; 72 for(int i=hd[u];i;i=e[i].nxt){ 73 int v=e[i].v; 74 if(d[v]==d[u]+1 && e[i].f){ 75 tmp=DFS(v,min(lim,e[i].f)); 76 e[i].f-=tmp; 77 e[i^1].f+=tmp; 78 f+=tmp; 79 lim-=tmp; 80 if(!lim)return f; 81 } 82 } 83 d[u]=0; 84 return f; 85 } 86 int Dinic(){ 87 int res=0; 88 while(BFS())res+=DFS(S,1e9); 89 return res; 90 } 91 int smm=0; 92 bool solve(int lim){ 93 int i,j; 94 memset(hd,0,sizeof hd); 95 mct=1; 96 for(i=1;i<=smm;i++)ins(S,i,1); 97 for(i=1;i<=n;i++)ins(smm+i,T,a[i]);//胜场 98 int hd=0; 99 for(i=1;i<=n;i++) 100 for(j=1;j<=i;j++){ 101 if(i==j)continue; 102 if(i<=lim && a[i]<a[j])ins(id[i][j],smm+i,1); 103 else{ 104 ins(id[i][j],smm+i,1); 105 ins(id[i][j],smm+j,1); 106 } 107 } 108 if(Dinic()==smm)return 1; 109 return 0; 110 } 111 int m; 112 int main() 113 { 114 scanf("%d\n",&m); 115 int i,j; 116 while(m--){ 117 init();// 118 read(); 119 sort(a+1,a+n+1,cmp); 120 init2(); 121 // for(i=1;i<=n;i++)printf("%d ",a[i]); 122 // printf("\n"); 123 smm=0; 124 for(i=1;i<=n;i++)smm+=a[i]; 125 if(smm!=n*(n-1)/2){printf("0\n");continue;} 126 smm=n*(n-1)/2; 127 S=0;T=smm+n+1; 128 int ans=0; 129 for(i=1;i<=n;i++){ 130 if(solve(i))ans=i; 131 else break; 132 } 133 printf("%d\n",ans); 134 } 135 return 0; 136 }
POJ2699 The Maximum Number of Strong Kings
标签:i++ max [] art nbsp http 复杂度 read sub
原文地址:http://www.cnblogs.com/SilverNebula/p/6146176.html