标签:http 训练 转化 com 计算 height 概念 转换 数量级
前边总结了线性SVM,最终转化为一个QP问题来求解。后来又考虑到非线性SVM,如果特征特别特别多的话,直接使用QP的话求解不了,我们经过一系列的转化,把这一问题转化为训练集大小n量级的QP问题。
http://www.cnblogs.com/futurehau/p/6143178.html
在之前的基础之上,我们继续学习,引入核函数的概念,完全避免了特征数目量级的计算问题。接下来依次分析polynomial Kernel, Gaussian Kernel,并对他们进行对比分析。
一、Kernel 的引入
之前我们得到对偶问题的QP形式:
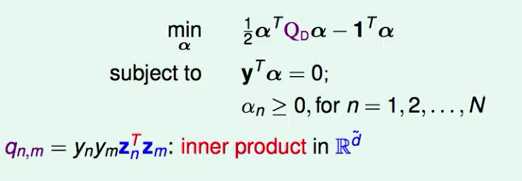
这似乎是一个n量级的问题,似乎和特征的个数无关,但是仔细一看,Q矩阵每一项的求解涉及到Z空间的内积,这就是特征个数量级的一个操作。所以我们从这里入手,想想怎样可以简化Z空间内积的计算呢?
以二次变换为例,我们把X空间映射到Z空间,我们现在看看Z空间上的内积表达式是什么,可以怎么转换到X空间上。

好了,我们发现Z空间上的内积刚好可以转换为X空间上的内积。所以我们就想,我们不需要显示的去先把X空间上的数据计算到空间上,然后训练参数,我们可以直接使用X空间上的参数来计算即可,这样大大降 低了我们的计算复杂度。
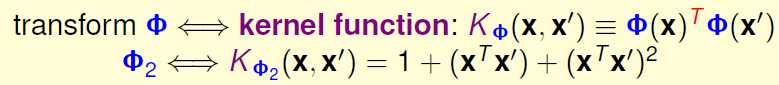
这样,上述的转换就叫做Kernel函数。它把之前变换后的空间Z上的内积运算转换为原空间上的内积运算。
我们再回过头来看看之前的对偶QP问题,Z空间上的哪些内积运算可以转换到X空间上呢?

这样一来,所有的训练,测试都没有直接在Z空间上进行内积运算,所有运算都转换到了X空间上。这样所有运算就和你的特征维度没有关系了。
二、pllynomial Kernel
三、Gaussian Kernel
四、Comparison of Kernels
标签:http 训练 转化 com 计算 height 概念 转换 数量级
原文地址:http://www.cnblogs.com/futurehau/p/6149558.html