标签:零空间 需要 1年 secondary 应用 它的 吴军 计算 思考
在很多线性代数问题中,如果我们首先思考若做SVD,情况将会怎样,那么问题可能会得到更好的理解[1]。
--Lloyd N. Trefethen & David Bau, lll
为了讨论问题的方便以及实际中遇到的大多数问题,在这里我们仅限于讨论实数矩阵,注意,其中涉及到的结论也很容易将其扩展到复矩阵中(实际上,很多教材采用的是复矩阵的描述方式),另外,使用符号 x,y 等表示向量,A,B,Q等表示矩阵。
首先给出正交矩阵的概念。所谓正交矩阵,即该矩阵不同的两个列向量之间作内积等于0(平面几何中垂直的定义在多维情形下推广),相同的列向量和自身做内积等于1(单位向量)。特别地,如果Q是一个n阶正交方阵,则Q‘Q=QQ‘=I, 即正交矩阵的转置即是该矩阵的逆矩阵。正交矩阵在数值分析中起着很重要的作用,一个主要的原因是它能够保持向量的2范数不变(因此SVD也常用于最小二乘问题的求解中),以及矩阵的2范数以及F范数不变,即||Qx||_2=||x||_2, ||AQ||_2=||A||_2,||QA||_F=||A||_F。
奇异值分解定理:对于任意一个 m*n 的实数矩阵 A,都存在 m*m 的正交矩阵 U 和 n*n 的正交矩阵V,以及 m*n 的对角矩阵 D=diag(d_1,d_2,...,d_r),使得
A = UDV‘
其中,d_1>=d_2>=...>=d_r>=0 称为奇异值,U和V的各列分别称为左奇异向量和右奇异向量。
下面给出SVD的几何意义,n 维单位向量 x 在任意的 m*n 矩阵 A=UDV‘ 下的像下是 m 维空间中的一个超椭球。具体地,正交变换V‘保持了x的向量长度不变,对角矩阵D将球面拉伸到一个超椭球上,最后正交变换U将旋转这个超椭球,但不改变它的形状,参见下图。
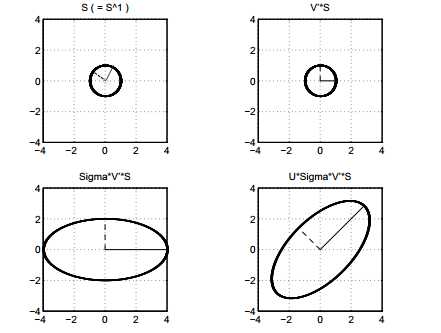
图1 SVD几何解释示意图[2]
奇异值分解的矩阵性质:
1. 矩阵 A 的秩等于非零奇异值的个数。
2. 矩阵 A 的值域空间等于由 U 的前 r 个列向量张成的空间,而 A 的零空间是由 V 的后面 n-r 个列向量张成的空间。
3. ||A||_2=d_1, ||A||_F=sqrt(d_1+...+d_r)。
4. A 的非零奇异值的平方等于 AA‘ 和 A’A 的非零特征值。
注意,一旦能够得到A的奇异值分解,按照上述给出的性质,那么关于A的秩,A的值域或者零空间的基,以及A的2-范数,F-范数等就自然地能够得到。从这方面来看,SVD可以看作是求解这些问题的一个工具。除此之外,它还被广泛地用来求解最小二乘问题,正则化问题,低秩逼近问题,数据压缩问题,文本处理中的分类问题[4]等。
细心的童鞋发现,上面的所有结论都是建立在SVD定理正确以及能够有效计算出给定矩阵A的SVD分解的基础上。关于第一个问题,可以使用数学归纳法进行证明[3];第二个问题,由于证明中采用了数学归纳法,显然它不能有效地求解出具体矩阵的SVD分解,而数值求解SVD需要借助于对称矩阵的特征值分解(一个简单的想法是对 AA‘ 进行特征值分解,然后得到 A 的奇异值分解,可惜该类方法数值稳定性较差,细节内容不展开叙述)。
最后,对矩阵的奇异值和矩阵的特征值之间的联系进行几点说明。第一,对于任意矩阵,都存在奇异值分解,而并非所有矩阵都存在特征值分解的;第二,奇异值分解中使用的是正交的矩阵,而特征值分解中使用的基一般不是正交的;第三,矩阵最小奇异值小于矩阵最小特征值的模长,矩阵最大奇异值大于矩阵最大奇异值的模长[5]。
参考文献:
[1] 数值线性代数 Chap4-5,L N. Trefethen,David Bau, lll 著,陆金甫,关治译,人民邮电出版社,2006年
[2] 应用数值线性代数,J W. Demmel著,王国荣译,人民邮电出版社,2007年
[3] 矩阵计算(第三版),Gene H.Golub,
[5] 矩阵A的特征值与奇异值大小关系? https://www.zhihu.com/question/40181430/answer/85446211
标签:零空间 需要 1年 secondary 应用 它的 吴军 计算 思考
原文地址:http://www.cnblogs.com/liuyc/p/6151892.html