标签:alt tle 技术 函数 汉诺塔 main printf pes key
理解递归的最重要的一点是不要去纠结递归函数中的一些细节到地是怎么实现的,这个例子在上一篇的汉诺塔问题中的到了充分的体现。
本篇文章只要是实现最大公倍数的递归实现方法。
最大公倍数是指两个数能够被一组数同时整除,其中最大的那个数就叫做最大公倍数,求解最大公倍数这里主要说两个想法,其实就是将复杂的问题简化逐步简化到一个很小的问题,然后求得答案。
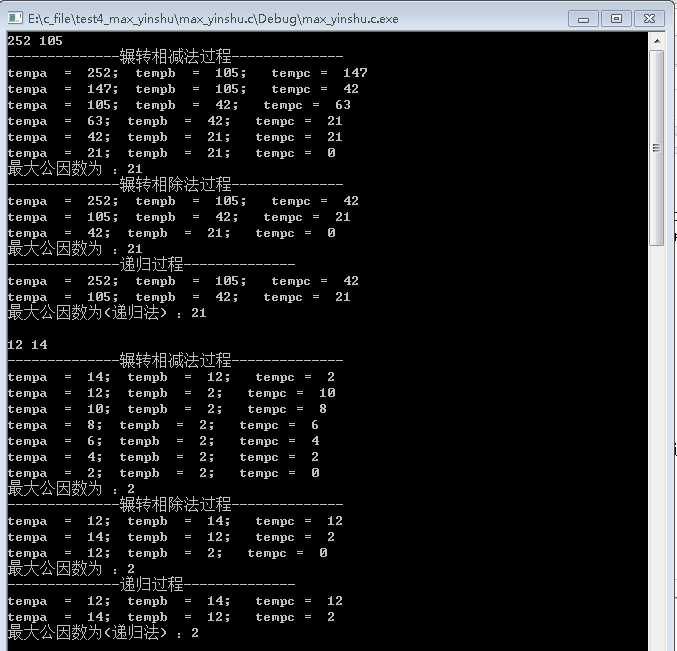
假设有两个数 252和105
252 : 21*12
105 : 21 * 5
252 - 105 = 147 = 21 * 7
两个数相减后他的最大公倍数是不变的,所以,可以用这种方法一直递减来实现算法
除法和递减的性质其实是一样的
#include "stdafx.h" //辗转相减法 int max_yinshu1(int a , int b){ int temp = 1; int tempa = a; int tempb = b; int tempc = 0; printf("--------------辗转相减法过程--------------\n"); while(tempa != 0){ if(tempa < tempb){tempc = tempa;tempa = tempb;tempb = tempc;} tempc = tempa - tempb; printf("tempa = %d; tempb = %d; tempc = %d\n" , tempa , tempb , tempc); tempa = tempc; } return tempb; } //辗转相除法 int max_yinshu2(int a , int b){ int temp = 1; int tempa = a; int tempb = b; int tempc = 0; printf("--------------辗转相除法过程--------------\n"); /*while(tempa != 0){ if(tempa < tempb){tempc = tempa;tempa = tempb;tempb = tempc;} tempc = tempa % tempb; printf("tempa = %d; tempb = %d; tempc = %d\n" , tempa , tempb , tempc); tempa = tempc; }*/ while(tempb != 0){ tempc = tempa % tempb; printf("tempa = %d; tempb = %d; tempc = %d\n" , tempa , tempb , tempc); tempa = tempb; tempb = tempc; } return tempa; } //递归法 int max_yinshu3(int a , int b){ if(a%b == 0) return b; else{ printf("tempa = %d; tempb = %d; tempc = %d\n" , a , b , a%b); return max_yinshu3(b , a%b); } } int _tmain(int argc, _TCHAR* argv[]) { int a = 0; int b = 0; int data1 = 0; int data2 = 0; int data3 = 0; while(scanf("%d%d" , &a , &b)){ data1 = max_yinshu1(a , b); printf("最大公因数为 :%d\n" , data1); data2 = max_yinshu2(a , b); printf("最大公因数为 :%d\n" , data2); printf("--------------递归过程--------------\n"); data3 = max_yinshu3(a , b); printf("最大公因数为(递归法) :%d\n" , data3); } return 0; }
标签:alt tle 技术 函数 汉诺塔 main printf pes key
原文地址:http://www.cnblogs.com/havihouston/p/6165243.html